Question

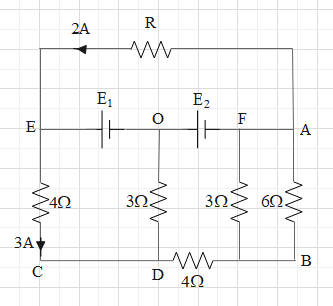
In the circuit shown in figure, ${{E}_{1}}$ and ${{E}_{2}}$ are two ideal sources of unknown emfs. Some currents are shown. Potential difference appearing across $6\Omega $ resistance is ${{V}_{A}}-{{V}_{B}}=10V$.

(This questions has multiple correct options)
$\text{A}\text{. The current in the 4}\Omega \text{ resistance between C and B is 5A}\text{.}$
$\text{B}\text{. The unknown emf }{{\text{E}}_{1}}\ \text{is 36V}\text{.}$
$\text{C}\text{. The unknown emf }{{\text{E}}_{2}}\ \text{is 54V}\text{.}$
 $\text{D}\text{. The resistance R is equal to 9}\Omega \text{.}$

Answer 1

Hint: The given problem has a very long solution since we have to find the values of many things. Make use of the Ohms’ law when required. We also need the junction law to solve this problem. Start with assuming the potential at anyone point as zero.

Formula used:
V = iR

Complete step-by-step answer:
In this solution we will be the junction law for current and the Ohm’s law. According to the Ohm’s law, the potential difference across a resistance R, through which a current I is flowing is given as V = iR.
Let us first assume that the potential at point O is zero. Then the potential at points A and F is ${{E}_{2}}$ , potential at point E is ${{E}_{1}}$.
It is given that the potential difference of the $6\Omega $ resistance is 10V. Then with ohm’s law, the current in this resistance is \[i=\dfrac{10}{6}=\dfrac{5}{3}A\]. The direction of this current is from A to B because the current always flows from the higher potential to a lower potential
Since the $3\Omega $ is parallel with this resistance, the potential difference will be 10V. In this resistance also the current will be in the downwards direction and its value will be $i=\dfrac{10}{3}A$.
Then from the junction law, we get that the current in the adjacent $4\Omega $ (between D and B) is $\dfrac{10}{3}+\dfrac{5}{3}=\dfrac{15}{3}=5A.$
Therefore, the current flowing in the $4\Omega $ resistance between C and B is 5A.
Hence, the option is true.
Now, the potential difference across this $4\Omega $ resistance will be $V=5(4)=20V$.
We know that the potential at A is ${{E}_{2}}$ and ${{V}_{A}}-{{V}_{B}}=10V$.
$\Rightarrow {{E}_{2}}-{{V}_{B}}=10V$
$\Rightarrow {{V}_{B}}={{E}_{2}}-10$ …. (i).
Form point B, there is a potential drop of 20V when we reach point D.
This means that ${{V}_{B}}-{{V}_{D}}=20V$ ….. (ii).
From (i) and (ii) we get,
${{E}_{2}}-10-{{V}_{D}}=20V$
$\Rightarrow {{V}_{D}}={{E}_{2}}-30$.
By applying junction law at point D, we get that the current in the $3\Omega $ is $3+5=8A$.
Then the potential difference across this resistance will be $8(3)=24V$.
This means that ${{V}_{D}}-{{V}_{O}}=24V$.
But ${{V}_{O}}=0V$and ${{V}_{D}}={{E}_{2}}-30$
\[\Rightarrow {{E}_{2}}-30=24V\].
\[\Rightarrow {{E}_{2}}=54V\]
Hence, option C is true.
The potential at C and D are equal.
$\Rightarrow {{V}_{C}}={{E}_{2}}-30=54-30=24V$.
And
${{V}_{E}}={{E}_{1}}$.
Therefore, the potential difference across the $4\Omega $ resistance is ${{E}_{1}}-24=12V$.
$\Rightarrow {{E}_{1}}-24=12V$
$\Rightarrow {{E}_{1}}=36V$.
Hence, option is B is true.
Now, the potential difference across the resistance R will be ${{E}_{2}}-{{E}_{1}}=2R$.
And
${{E}_{2}}-{{E}_{1}}=54-36=18V$
$\Rightarrow 18=2R$
$\Rightarrow R=9\Omega $.
Hence, option D is also true.
Therefore, the correct options are A, B, C and D.

So, the correct answers are “Option A,B,C and D”.

Note: We have solved the question by using Ohm’s law and junction law. One can use the Kirchhoff‘s voltage law for the required loops. The law is also called a loop law.
Remember that current always flows higher potential to a lower potential. Hence, there is a potential drop across a resistance in the direction of the current.