Question

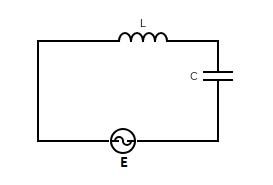
In the circuit shown here, the voltage across $L$ and $C$ are respectively $300V$ and $400V$. The voltage $E$ of the ac source is.

A) \[400V\]
B) \[500V\]
C) \[100V\]
D) \[700V\]

Answer 1

Hint: Inductance opposes the change in the current and serves to delay the decrease or increase of current in the circuit. This causes the circuit current to lag behind the applied voltage in an inductive circuit. Capacitance opposes the change in voltage and serves to delay the increase or decrease of voltage across the capacitor. This causes the voltage to lag behind the current in a capacitive circuit.

Complete step by step solution:
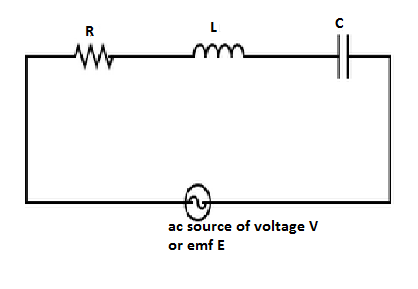
Consider a circuit containing an inductor, capacitor, and resistor connected in series across an alternating source of voltage $V$ or emf $\varepsilon $.

Let the source supplies a sinusoidal voltage which is given by,
$V = {V_0}\sin \omega t$
Where, ${V_0}$ is the peak value of voltage $\omega $ is the angular frequency and $t$ is the time period.
Let $q$ be the charge on the capacitor and $I$ be the current in the circuit at any instant of time $t$.
Let ${V_R},{V_L},{V_C}$ represent the voltage across the resistor, inductor, and capacitor respectively.
Then, voltage across resistor, ${V_R} = {i_0}R$
Voltage across inductor, ${V_L} = {i_0}{X_L}$
Voltage across capacitor, ${V_C} = {i_0}{X_C}$
Where, ${i_0}$ is the peak value of current, ${X_C}$ is capacitive reactance, ${X_L}$ is the inductive reactance and R is the resistance of the resistor.
Then net voltage or emf is given by,$V$ or$\varepsilon = \sqrt {\left( {{V_R}^2 + {{\left( {{V_C} - {V_L}} \right)}^2}} \right)} $ …………….(1)
Now from the given question, we have an inductor and capacitor connected in series to the ac source.

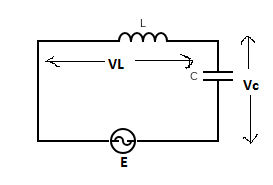
Then, voltage across capacitor, ${V_c} = 400V$
Voltage across inductor, ${V_L} = 300V$
Here resistor is not connected thus we can neglect the term voltage across capacitor, ${V_R}$
Then from equation (1) we get, $\varepsilon = \sqrt {{{\left( {{V_C} - {V_L}} \right)}^2}} $
Now substituting the given values we get,
$\varepsilon = \sqrt {{{\left( {400 - 300} \right)}^2}} $
$\varepsilon = \sqrt {{{100}^2}} = 100V$

$\therefore $ The voltage $E$ of the ac source is $100V$.

Additional information:
The opposition offered by an inductor for the flow of ac is called ‘inductive reactance’.
An alternating voltage is one whose magnitude changes with time and direction changes periodically.
The frequency of the direct current is zero. That is direct current is independent of frequency.

Note:
When $L$ or $C$ present in an ac circuit, energy is required to build up a magnetic field around l or electric field in $C$. This energy comes from the source. However, the power consumed in $L$ or $C$ is zero because all the power received from the source in a quarter cycle is returned to the source in the next quarter cycle. This power oscillates back and forth and is called reactive power. The total opposition to alternating current in an AC circuit is called impedance of the circuit $Z$.