Question

In the circuit diagram shown all the capacitors are in $\mu F$. The equivalent capacitance between points A and B is $(in\,\mu F)$ :

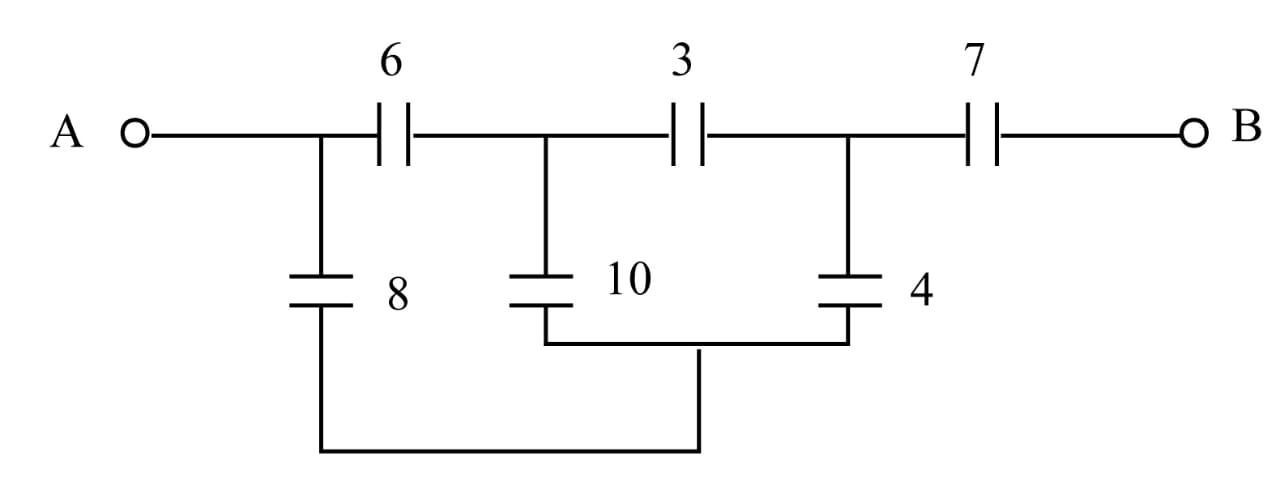
\[\begin{array}{l}
A.\,\dfrac{{14}}{5}\\
B.\,7.5\\
C.\,\dfrac{3}{7}\\
D.None of these
\end{array}\]

Answer 1

Hint: In this question we have to apply the concept of the combination of capacitors in parallel and series circuits. We have to convert the given circuit in a form in which we can apply the formulas of the combination of capacitors in parallel and series circuits.

Complete step by step answer:
We will mark the junction points on the above circuit.

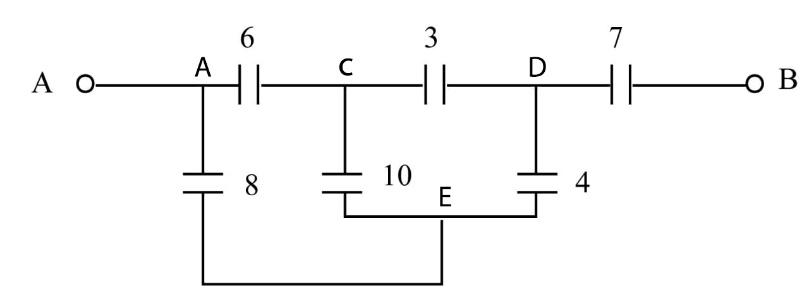
Now that we have marked each and every junction in the circuit, we will try to redraw the diagram and convert it into a more simplified circuit so that we can apply the formulas of the combination of capacitors. We will plot all the junction points and we will connect the junction points with capacitors according to the circuit given the question.

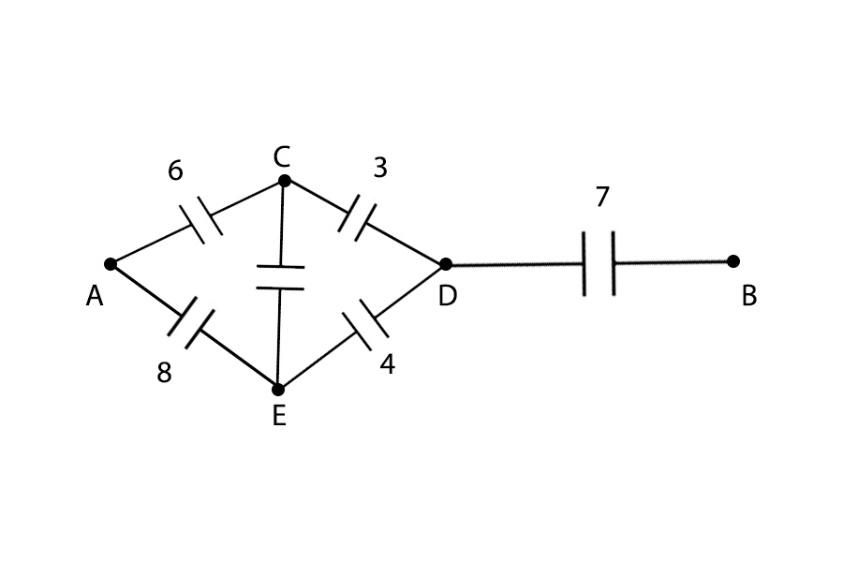
We have drawn the given circuit by seeing the junction names we marked earlier. By seeing the above circuit, we can see a Wheatstone bridge structure. Therefore, let us apply the condition for a balanced Wheatstone Bridge:
If the following condition is satisfied,
$\dfrac{{{C_1}}}{{{C_2}}} = \dfrac{{{C_3}}}{{{C_4}}}$
Then the capacitor in the mid junction can be ignored. Therefore:

$\dfrac{6}{3} = \dfrac{4}{8} = 2$
Hence the condition is true, and the mid junction can be ignored, therefore the circuit now becomes:

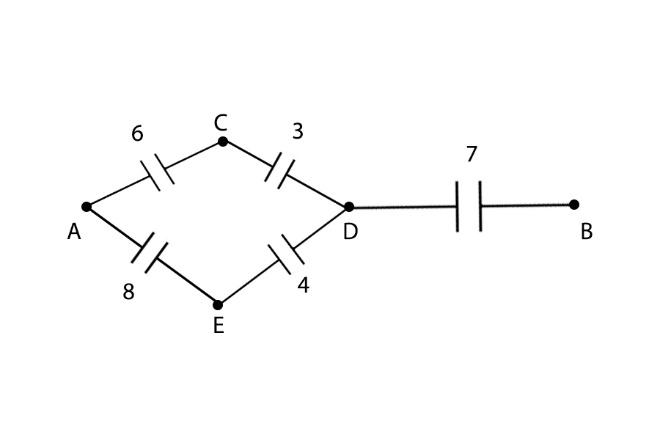
We can see that the resistors between A and C are in series and the resistors between B and D are in series.
And both branches are parallel to each other.
Calculating the resistance in this parallel branch we get:

For the upper branch, the capacitance:
$
\dfrac{1}{{{C_{eq}}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}}\\
\implies \dfrac{1}{{{C_{eq}}}} = \dfrac{1}{6} + \dfrac{1}{3}\\
\implies \dfrac{1}{{{C_{eq}}}} = \dfrac{9}{{18}}\\
\implies {C_{eq}} = 2\mu F
$

Similarly, the capacitance of the lower branch:
$
\dfrac{1}{{{C_{eq}}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}}\\
\implies \dfrac{1}{{{C_{eq}}}} = \dfrac{1}{4} + \dfrac{1}{8}\\
\implies \dfrac{1}{{{C_{eq}}}} = \dfrac{{12}}{{32}}\\
\implies {C_{eq}} = \dfrac{8}{3}\mu F
$

Now these two branches are in parallel to each other so their equivalent capacitance is:
$
{C_{Parallel}} = 2 + \dfrac{8}{3}\\
\implies {C_{Parallel}} = \dfrac{{14}}{3}\mu F
$

 Now this whole parallel combination is in series with another capacitance of $7\mu F$, therefore the final equivalent capacitance:
$
\dfrac{1}{{{C_{eq}}}} = \dfrac{1}{{\dfrac{{14}}{3}}} + \dfrac{1}{7}\\
\implies \dfrac{1}{{{C_{eq}}}} = \dfrac{3}{{14}} + \dfrac{1}{7}\\
\implies \dfrac{1}{{{C_{eq}}}} = \dfrac{{3 + 2}}{{14}}\\
\implies {C_{eq}} = \dfrac{{14}}{5}\mu F
$

Hence the final answer of the question is $\dfrac{{14}}{5}\mu F$. And the correct option is (A).

Note:
These types of questions require the understanding of students regarding the combination of circuits. Also, while redrawing or reconstructing a circuit, some special cases like Wheatstone Bridge can arise therefore the student should know about these kinds of cases and the condition regarding these conditions. Also, while doing the calculation of the capacitance we should keep in mind that the formulas of capacitance of series and parallel are reverse of that of the resistors. And most of the students get confused about this and end up getting the wrong answer.