Question

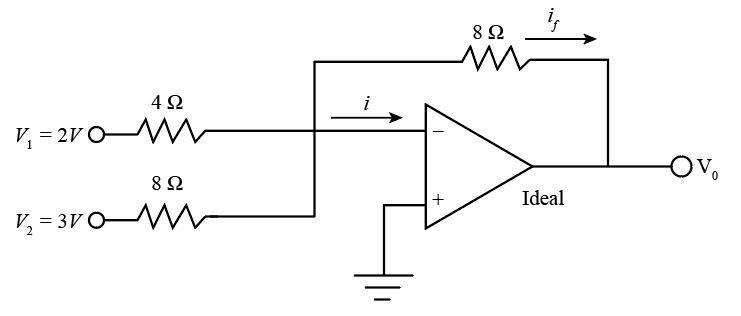
In the below figure, find the output voltage, if the op-amp is ideal

A.$ - 7\;{\rm{V}}$
B.$ - 6\;{\rm{V}}$
C.$ - 1\;{\rm{V}}$
D.$6\;{\rm{V}}$

Answer 1

Hint: To find the output voltage, we will use Ohm's law at different points of the circuit. Since the resistors are in parallel at the input terminal, we will find the current flowing through the respective resistance and then will add the current to find the final current flowing through the resistor at the output terminal. Then with the help of this final current and the resistance at the output terminal, we will find the output voltage.

Complete step by step answer:
Given:
The circuit consists of three resistors ${R_1} = 4\;\Omega $ ,${R_2} = 8\;\Omega $ and ${R_f} = 8\;\Omega $ .
The voltages at the input terminal are ${V_1} = 2\;{\rm{V}}$ , ${V_2} = 3\;{\rm{V}}$ and represents the voltage at the output terminal.
We can write the expression for current flowing through resistor ${R_1}$ from the ohm’s law as
${V_1} = {i_1}{R_1}$
We rearrange the above expression as
${i_1} = \dfrac{{{V_1}}}{{{R_1}}}$
Similarly, we can write the expression for current flowing through resistor ${R_2}$ from the ohm’s law as
${V_2} = {i_2}{R_2}$
We rearrange the above expression as
${i_2} = \dfrac{{{V_2}}}{{{R_2}}}$
Since resistance ${R_1}$and ${R_2}$are parallel so the current ${i_1}$ and ${i_2}$ will add up to give the final current ${i_f}$ which can be expressed as:
${i_f} = \dfrac{{{V_1}}}{{{R_1}}} + \dfrac{{{V_2}}}{{{R_2}}}$
We will substitute $4\;\Omega $ for ${R_1}$ , $8\,\Omega $ for ${R_2}$ , $3\;{\rm{V}}$ for ${V_1}$ and $2\;{\rm{V}}$ for ${V_2}$ in the above expression.

$\begin{array}{l}
{i_f} = \dfrac{{3\;{\rm{V}}}}{{8\;\Omega }} + \dfrac{{2\;{\rm{V}}}}{{4\;\Omega }}\\
{i_f} = \left( {\dfrac{{3 + 4}}{8}} \right)\;{\rm{A}}\\
{i_f} = 0.875\;{\rm{A}}
\end{array}$
Now to find the value of ${V_o}$, we will write the relation between ${i_f}$ and ${R_f}$ from the ohm’s law and from the above figure.
${V_o} = - {i_f}{R_f}$
We will substitute $8\,\Omega $ for ${R_f}$and $0.875\;{\rm{A}}$for ${i_f}$in the above expression.
$\begin{array}{l}
{V_o} = - \left( {8\,\Omega } \right)\left( {0.875\;{\rm{A}}} \right)\\
{V_o} = - 7\;{\rm{V}}
\end{array}$
Therefore, the output voltage in the op-amp is $ - 7\;{\rm{V}}$

So, the correct answer is “Option A”.

Note:
Op-amp stands for operational amplifier. It can be categorised as a device which amplifies voltage and works with the external feedback components like resistors or capacitors from its input terminal to output terminal. This amplifier gives response only to the difference between voltages and doesn’t consider their individual values. The current at the input terminal is zero since it has high impedance.