Question

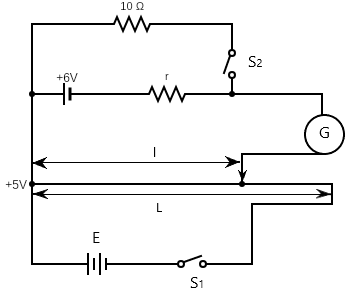
In the arrangement shown in figure when the switch $ {S_2} $ is open, the galvanometer shows no deflection for $ l = \dfrac{L}{2} $ . When the switch $ {S_2} $ is closed, the galvanometer shows no deflection for $ \dfrac{{5L}}{{12}} $ . The internal resistance $ \left( r \right) $ of 6V cell and the emf $ E $ of the other battery respectively are

(A) $ 3\Omega ,8{\text{V}} $
(B) $ 2\Omega ,12{\text{V}} $
(C) $ 2\Omega ,24{\text{V}} $
(D) $ 3\Omega ,12{\text{V}} $

Answer 1

Hint: When galvanometer shows no deflection, it means no current is flowing through it. In this case the ratio of voltage across the wire to the point where the jockey is to the voltage across the entire wire is equal to the ratio of the length to the jockey is to the ratio of the entire length of the potentiometer.

Formula used: In this solution we will be using the following formulae;
 $ \dfrac{{{E_1}}}{{{E_2}}} = \dfrac{{{L_1}}}{{{L_2}}} $ where $ {E_1} $ is the voltage across the potentiometer to where the jockey is, $ {E_2} $ is the voltage across the entire potentiometer, $ {L_1} $ is the length of the wire of the potentiometer to where the jockey is, and $ {L_2} $ is the length of the entire wire.

Complete step by step answer:
When the switch $ {S_2} $ is closed, no current will flow through the section of the circuit. Now at the same time, no deflection in the galvanometer if the jockey is at $ l = \dfrac{L}{2} $ . At this point, we can use the equation
 $ \dfrac{{{E_1}}}{{{E_2}}} = \dfrac{{{L_1}}}{{{L_2}}} $ where $ {E_1} $ is the voltage across the potentiometer to where the jockey is, $ {E_2} $ is the voltage across the entire potentiometer, $ {L_1} $ is the length of the wire of the potentiometer to where the jockey is, and $ {L_2} $ is the length of the entire wire. Hence,
 $ \dfrac{6}{E} = \dfrac{{\dfrac{L}{2}}}{L} $
Simplifying, and calculating for $ E $ , we have
 $ E = 12{\text{V}} $ .
Also, there is no deflection when the switch $ {S_2} $ is closed at $ l = \dfrac{{5L}}{{12}} $ , however current will flow through the upper branch of the circuit.
Applying kirchoff’s rule to that circuit, we have
 $ 6 - Ir - 10I = 0 $
 $ \Rightarrow I = \dfrac{6}{{r + 10}} $
Hence, the voltage from the cell to beyond the internal resistance is
 $ V = 6 - Ir = 6 - \dfrac{{6r}}{{r + 10}} $
Now, because there’s no deflection in galvanometer, we have
 $ \dfrac{V}{E} = \dfrac{{\dfrac{{5L}}{{12}}}}{L} $ . replacing $ E $ with 12 volts and finding $ V $ , we have that
 $ V = 5{\text{V}} $
Hence,
 $ 6 - \dfrac{{6r}}{{r + 10}} = 5 $
 $ \Rightarrow \dfrac{{6r}}{{r + 10}} = 1 $
Solving for $ r $ , we have
 $ r = 2\Omega $
Hence, the correct option is B.

Note:
For clarity, observe that the internal resistance does not affect the emf of the 6 V cell in the first case but is affected in the second case. This is because in the first case, current is not flowing through the cell, thus the internal resistance is dormant.