Question

In the adjoining figure, the radius of the inner circles, if other circles are of m units is

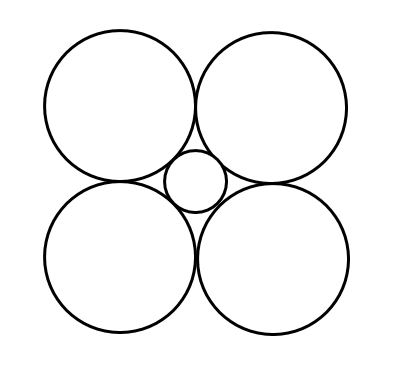
A. $$\left(\sqrt{2}-1\right)m$$
B. $$\sqrt{2}m$$
C. $${\displaystyle \frac{1}{\sqrt{2}}}m$$
D. $${\displaystyle \frac{1}{\sqrt{2+1}}}m$$

Answer 1

Hint: First of all, redraw the figure of this problem by joining all the centres of the outer circles to form a square of side length $$2m$$ units. Then find the length of its diagonal and equate it to the sum of the radius of the two outer circles and the diameter of the inner circle to reach the solution of the given problem.

Complete step by step solution:
If we join all the centres of the four outer circles then it forms a square of side $$2m$$ units as shown in the given below figure:

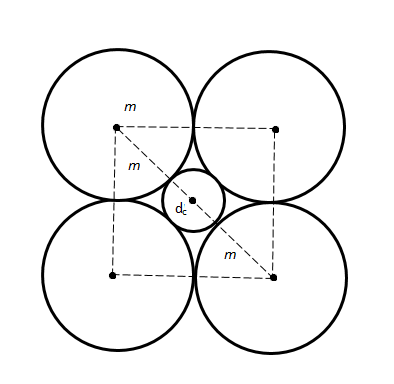
We know that the diagonal of the square of side $$a$$ units is given by $$\sqrt{2}a$$ units.
Thus, the length of the diagonal formed is $$2\sqrt{2}m$$ units.
Clearly from the figure, the diagonal of the square passes through the centre of the inner circle and the length of the diagonal is equal to the sum of radius of the two outer circles and the diameter of the inner circle.
Let $$d_c$$ be the length of the diameter of the inner circle.
So, we have $$2\sqrt{2}m=m+d_c+m$$
$$\begin{gathered} \Rightarrow 2\sqrt{2}m=2m+d_c \\ \Rightarrow d_c=2\sqrt{2}m-2m \\ \therefore d_c=2m\left(\sqrt{2}-1\right) \end{gathered}$$
We know the radius of a circle is equal to half of the length of its diameter.
Hence, the radius of inner circle $$=\frac{d_c}{2}=\frac{2m\left(\sqrt{2}-1\right)}{2}=\left(\sqrt{2}-1\right)m$$
Thus, the correct option is A. $$\left(\sqrt{2}-1\right)m$$

Note: The diagonal of the square of side $$a$$ unit is given by $$\sqrt{2}a$$ units. In this problem the obtained radius of the inner circle should be less than the radius of the outer circle as this smaller circle is surrounded by the bigger circles. In this way we can check if our answer is correct or not.