
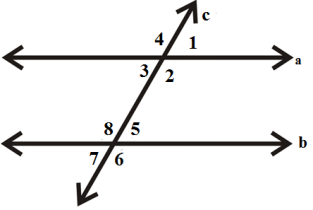
In the adjoining figure, identify the pair of corresponding angles.

Answer
581.7k+ views
Hint:- When two lines intersect by another line, the angles in matching corners are called corresponding angles.
Complete step by step by solution
In the above figure a, b are two parallel lines, which are crossed by a transversal line called c. Line and c form angles\[{\text{1}},{\text{ 2}},{\text{ 3 and 4}}\]. Similarly line b and line c form angles 5,6,7,8.
Now according to hint in the figure \[{\text{angle }}\left( {{\text{1}},{\text{ 3}}} \right),{\text{ angle }}\left( {{\text{2}},{\text{ 4}}} \right),{\text{ angle }}\left( {{\text{5}},{\text{ 6}}} \right){\text{ and angle }}\left( {{\text{7}},{\text{ 8}}} \right)\]are corresponding angles.
Therefore, here we have four pairs of corresponding angles, which are\[\left( {{\text{1}},{\text{ 3}}} \right),{\text{ }}\left( {{\text{2}},{\text{ 4}}} \right),{\text{ }}\left( {{\text{5}},{\text{ 6}}} \right){\text{ and }}\left( {{\text{7}},{\text{ 8}}} \right)\].
As we know corresponding angles are always equal so these four pairs of angles are equal.
So, these four pairs of angles are equal.
i.e. $\angle 1 = \angle 3, \angle 2 = \angle 4, \angle 5 = \angle 6and\angle 7 = \angle 8$
Note –If two lines which are crossed by a transversal line are parallel, then the corresponding angles are equal.
Hence, here all corresponding angles are equal.
Complete step by step by solution
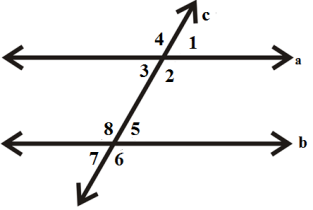
In the above figure a, b are two parallel lines, which are crossed by a transversal line called c. Line and c form angles\[{\text{1}},{\text{ 2}},{\text{ 3 and 4}}\]. Similarly line b and line c form angles 5,6,7,8.

Now according to hint in the figure \[{\text{angle }}\left( {{\text{1}},{\text{ 3}}} \right),{\text{ angle }}\left( {{\text{2}},{\text{ 4}}} \right),{\text{ angle }}\left( {{\text{5}},{\text{ 6}}} \right){\text{ and angle }}\left( {{\text{7}},{\text{ 8}}} \right)\]are corresponding angles.
Therefore, here we have four pairs of corresponding angles, which are\[\left( {{\text{1}},{\text{ 3}}} \right),{\text{ }}\left( {{\text{2}},{\text{ 4}}} \right),{\text{ }}\left( {{\text{5}},{\text{ 6}}} \right){\text{ and }}\left( {{\text{7}},{\text{ 8}}} \right)\].
As we know corresponding angles are always equal so these four pairs of angles are equal.
So, these four pairs of angles are equal.
i.e. $\angle 1 = \angle 3, \angle 2 = \angle 4, \angle 5 = \angle 6and\angle 7 = \angle 8$
Note –If two lines which are crossed by a transversal line are parallel, then the corresponding angles are equal.
Hence, here all corresponding angles are equal.
Recently Updated Pages
Master Class 9 Social Science: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Which places in India experience sunrise first and class 9 social science CBSE

What is the full form of pH?

Name 10 Living and Non living things class 9 biology CBSE

Write the 6 fundamental rights of India and explain in detail

What is pollution? How many types of pollution? Define it




