Question

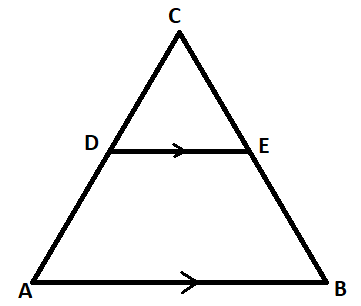
In the adjoining figure, $DE\parallel AB,$ $AD = 7$cm, $CD = 5$cm and $BC = 18$cm. Find BE and CE.

Answer 1

Hint: First of all this is a very simple problem, and to solve such kind of problems, we should be familiar with some basic concepts or properties of a triangle, there are three properties. First property is that the triangles drawn between two parallel lines with the same base have equal areas. The second property is that the ratio of areas of triangles with equal height is equal to the ratio of their bases, as the area of a triangle is the half of product of base and height. The third property is the basic proportionality theorem which describes that a line parallel to one side of a triangle divides the other two sides in equal proportion.

Complete step by step answer:
Here applying the basic proportionality theorem which states that if a line is drawn parallel to one side of a triangle and it intersects the other two sides at two distinct points, then it divides the two sides in the same ratio.
Hence using the basic proportionality theorem here, for the triangle ABC, as given below:
\[ \Rightarrow \dfrac{{CD}}{{CA}} = \dfrac{{CE}}{{CB}} = \dfrac{{DE}}{{AB}}\]
Given that $DE\parallel AB$.
Given that $AD = 7$cm and $CD = 5$cm
Also given that $BC = 18$cm.
Now substituting the values in the basic proportionality theorem, as given below:
$ \Rightarrow \dfrac{{CD}}{{CA}} = \dfrac{{CE}}{{CB}}$
As $CA = CD + AD$
$ \Rightarrow CA = 5 + 7$
$\therefore CA = 12$
$ \Rightarrow \dfrac{5}{{12}} = \dfrac{{CE}}{{18}}$
$ \Rightarrow \dfrac{{5(18)}}{{12}} = CE$
$\therefore CE = 7.5$
And given that $BC = 18$
$ \Rightarrow BC = CE + BE$
We found out that $CE = 7.5$, substituting the above expression to find the value of EB, as given below:
$ \Rightarrow 18 = 7.5 + BE$
$ \Rightarrow BE = 18 - 7.5$
$\therefore BE = 10.5$

Hence, CE=7.5cm and BE=10.5cm

Note: This problem can be done by applying the same basic proportionality theorem, but in a different way which gives you the same solution at the end. Given that DE is parallel to AB, then it can also be done by equating the ratio of CD to DA and CE to EB, which is expressed mathematically as: $\dfrac{{CD}}{{DA}} = \dfrac{{CE}}{{EB}}$, which also holds true for a basic proportionality theorem.