Question

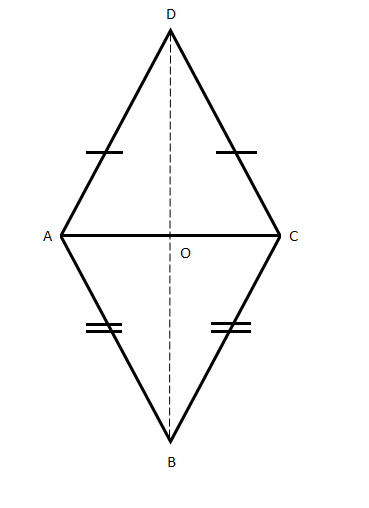
In the adjoining figure, \[AC\] and \[BD\] intersect at \[O\]. \[AB = CB,AD = CD\] and \[AO = OC\].
(a) Write the triangle congruent to \[\Delta AOD\].
(b) Write the triangle congruent to \[\Delta AOB\].
(c) Find the measure of \[\angle AOD\].

Answer 1

Hint: First of all, observe the given figure cleanly and then see that which triangle is going to be congruent with the given triangles. Use SSS congruence rule to show the triangles are congruent. So, use this concept to reach the solution of the given problem.

Complete step by step solution:
(a)
From the figure,
In \[\Delta AOD\] and \[\Delta COD\]
\[
   \Rightarrow AD = CD{\text{ }}\left[ {{\text{Given}}} \right] \\
   \Rightarrow AO = OC{\text{ }}\left[ {{\text{Given}}} \right] \\
   \Rightarrow OD = OD{\text{ }}\left[ {{\text{common}}} \right] \\
\]
Therefore, by SSS congruence rule \[\Delta AOD \cong \Delta COD\]
Thus, the triangle congruent to \[\Delta AOD\] is \[\Delta COD\]
(b)
From the figure,
In \[\Delta AOB\] and \[\Delta COB\]
\[
   \Rightarrow AB = CB{\text{ }}\left[ {{\text{Given}}} \right] \\
   \Rightarrow AO = OC{\text{ }}\left[ {{\text{Given}}} \right] \\
   \Rightarrow OB = OB{\text{ }}\left[ {{\text{common}}} \right] \\
\]
Therefore, by SSS congruence rule \[\Delta AOB \cong \Delta COB\].
Thus, the triangle congruent to \[\Delta AOB\] is \[\Delta COB\].
(c)
From the figure,
In \[\Delta ABD\] and \[\Delta CBD\]
\[
   \Rightarrow AB = CB \\
   \Rightarrow AD = CD \\
   \Rightarrow BD = BD \\
\]
Therefore, by SSS congruence rule \[\Delta ABC \cong \Delta CBD\]
By CPCT, \[\angle ABD = \angle CBD\]
Hence, \[BD\] divides \[\angle ABC\] into two equal parts i.e., \[BD\] bisects \[\angle ABC\].
\[\therefore \angle AOD = {90^0}\]

Note: In two triangles, if the three sides of one triangle are equal to the corresponding three sides (SSS) of the other triangle, then the two triangles are said to be in congruent by SSS congruence rule or criterion.