Question

In the adjoining circuit, initially, the switch S is open. The switch S is closed at \[t = 0\]. The difference between the maximum and minimum current that can flow in the circuit is

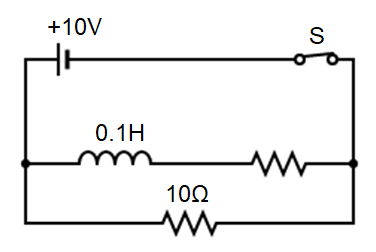
(A) 2 Amp

(B) 3 Amp

(C) Amp

(D) Nothing can be concluded

Answer 1

Hint: The inductor does not resist flow of a direct current, hence, acts as a closed circuit. Then the two 10 ohms resistors will simply be in parallel to one another.
Formula used: In this solution we will be using the following formulae;
\[\dfrac{1}{{{R_{eqp}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}\] where \[{R_{eqp}}\] is the equivalent resistance of two resistors in parallel, \[{R_1}\] is the resistance of one, and \[{R_2}\] is the resistance of the other resistor.
\[V = IR\]where\[V\] is the voltage across a resistor, \[I\] is the current flowing through the resistor, and \[R\] is the resistance of the resistor.

Complete Step-by-Step solution:
To solve the above question, we note that the inductor will not resist the flow of the current of a steady electricity (dc). Hence, we can view the inductor as non-existent, replacing it with a closed switch or wire.
Doing that, we would observe that the two 10 ohms resistors are simply in parallel to each other. Hence, we shall find the equivalent resistance. The equivalent resistance of two resistors in parallel can be given as
\[\dfrac{1}{{{R_{eqp}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}\] where \[{R_{eqp}}\] is the equivalent resistance of two resistors in parallel, \[{R_1}\] is the resistance of one, and \[{R_2}\] is the resistance of the other resistor.
Hence, inserting the known values, we have
\[\dfrac{1}{{{R_{eqp}}}} = \dfrac{1}{{10}} + \dfrac{1}{{10}} = \dfrac{2}{{10}}\]
Hence,
\[{R_{eqp}} = \dfrac{{10}}{2} = 5\Omega \]
Now, using the ohm's law, given by
\[V = IR\]where\[V\] is the voltage across a resistor, \[I\] is the current flowing through the resistor, and \[R\] is the resistance of the resistor.
We have,
\[10 = 5I\]
Then,
\[I = 2{\text{A}}\]
Hence, the correct answer is A

Note: For understanding and completeness, observe that since the current is a direct one, the graph will be a straight line as shown in A. Also, the minimum current hence is zero and which makes the difference between minimum and maximum 2 A.