Question

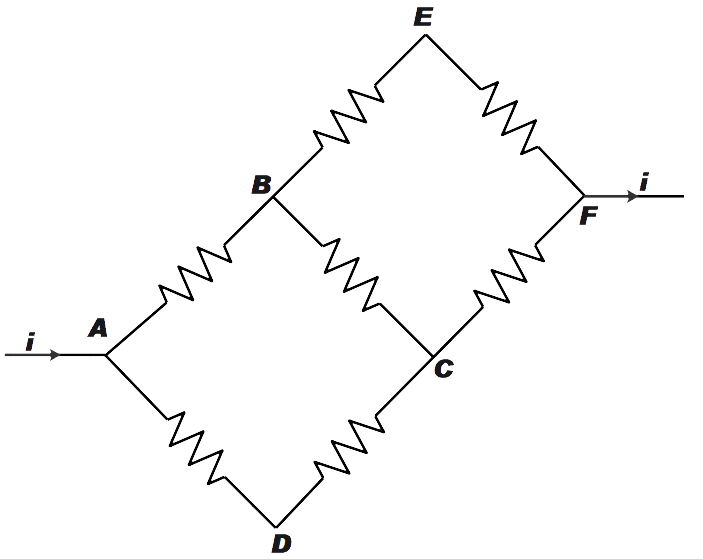
In the adjoining circuit diagram each resistance is of 10 \[\Omega \]. The current in the arm AD will be.

                   

A. \[\dfrac{2i}{5}\]
B. \[\dfrac{3i}{5}\]
C. \[\dfrac{4i}{5}\]
D. \[\dfrac{i}{5}\]

Answer 1

Hint: In this question we have been given a circuit diagram and to calculate the value of current in the arm AD of the given circuit diagram. We have been given that the resistance of each resistor in the diagram is 10 ohms. Therefore, we shall be using Kirchhoff’s law and loop rule to solve this question. Kirchhoff’s loop rule suggests that the sum of potential difference in any loop must be zero.

Complete answer:
From the given diagram, it is said that every resistor has the resistance of 10 ohms. Let us assume that the voltage applied is V
Also, let the current in the arm AB, AD and BC be \[{{i}_{1}}\], \[{{i}_{2}}\] and \[{{i}_{3}}\] respectively. Now, from the diagram we can say that, the current through arm BE and CF is \[{{i}_{1}}-{{i}_{3}}\] and \[{{i}_{1}}+{{i}_{2}}\] respectively.
Now, let the potential at point A be V
From Kirchhoff’s law we know,
\[i={{i}_{1}}+{{i}_{2}}\]
Now, we know that potential at point C must be equal.
Therefore, we can say
\[V-iR-{{i}_{3}}R=V-2{{i}_{2}}R\]
On solving
We get,
\[{{i}_{1}}+{{i}_{3}}=2{{i}_{2}}\]
Now, we also know that potential at point should also be equal from both sides
Therefore,
\[V-iR-({{i}_{1}}-{{i}_{3}})2R=V-2{{i}_{2}}R\]
On solving
We get,
\[i{{}_{1}}+({{i}_{1}}-{{i}_{3}})2=2{{i}_{2}}+({{i}_{1}}+{{i}_{3}})\]
Therefore,
\[3{{i}_{1}}-2{{i}_{3}}=3{{i}_{2}}+{{i}_{3}}\]
On solving
\[{{i}_{1}}={{i}_{3}}+{{i}_{2}}\]
After substituting the value of \[{{i}_{3}}\]from
We get,
\[{{i}_{1}}=2{{i}_{2}}-{{i}_{1}}+{{i}_{2}}\]
Therefore,
\[2{{i}_{1}}=3{{i}_{2}}\]
Now, after substituting the value of \[{{i}_{1}}\] from
\[2i-2{{i}_{2}}=3{{i}_{2}}\]
On solving
We get,
\[{{i}_{2}}=\dfrac{2i}{5}\]

So, the correct answer is “Option A”.

Note:
Kirchhoff’s loop rule also called as Kirchhoff’s Voltage law states that the sum of all the electric potential differences around a loop is zero. While applying the loop rule, we must first select a closed loop and decide the direction to go around the loop. The loop rule suggests that when a charge goes around a loop in a circuit and then returns to its starting point the potential energy of the charge must be the same as the charge is moving through the potential differences in the selected loop.