Question

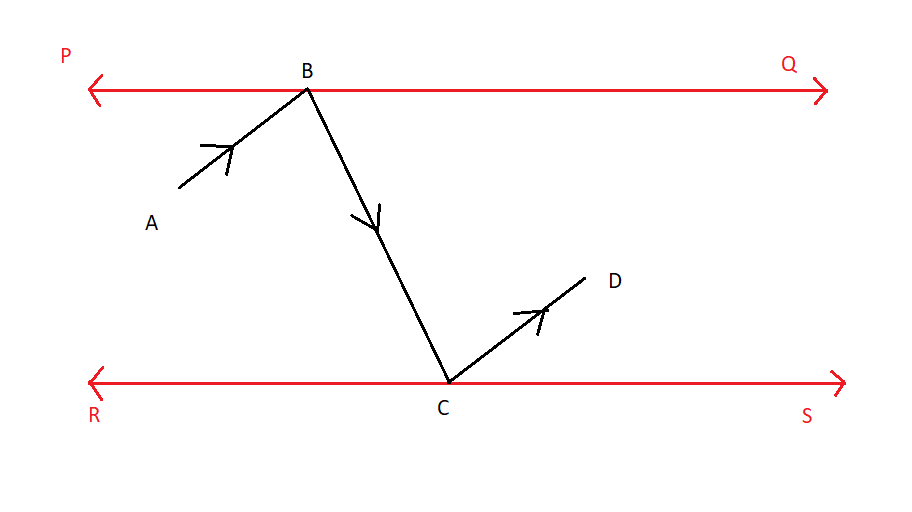
In the adjacent figure \[PQ\] and \[RS\] are two mirrors placed parallel to each other. An incident ray $\overrightarrow {AB} $strikes the mirror \[PQ\] at \[B\] , the reflected ray moves along the path $\overrightarrow {BC} $ and strikes the mirror \[RS\] at C and again reflected along $\overrightarrow {CD} $. Prove that \[AB||CD\].

Answer 1

Hint: When any two parallel lines are intersected by another line called transversal, many angles are formed. These angles are related to each other and are equal, namely, corresponding angles, alternate interior angles, alternate exterior angles, and consecutive interior angles. So, to prove any two lines parallel we can make these angles equal.

Complete step by step solution:

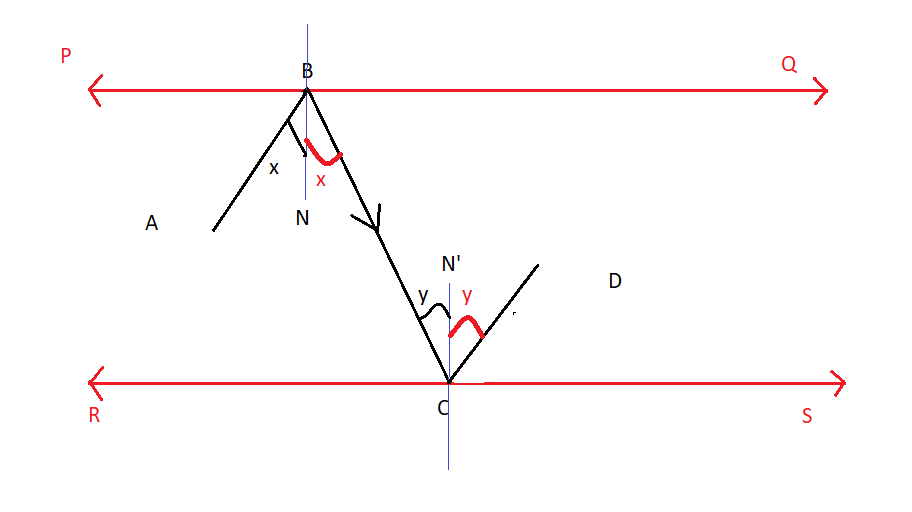
Here we draw perpendicular \[BN\] and \[CN'\] on a mirror \[PQ\] and \[RS\] . \[PQ\] is a mirror. So, the angle of incidence is equal to the angle of reflection.
Therefore, $\angle ABN = \angle NBC$ ………………(1)
Similarly, \[RS\] is a mirror. Therefore,
$\angle BCN' = \angle N'CD$……………(2)
So, \[BN\] is parallel to \[CN'\] . Let us take \[BC\] as a transversal.
$\angle NBC = \angle N'CB$ alternate interior angle………………(3)
Now, considering equations (1), (2), and (3), we can write the following, using the figure.
$\angle ABC = \angle BCD$
Hence, we can say that \[AB\] and \[CD\] are parallel rays.

Note:
A mirror angle of incidence is always equal to the angle of reflection. This is due to the laws of reflection. Which also states that the angle of incidence, angle of reflection, and normal lie on the same plane.
A Transversal is a line that intersects the two lines at two different points. These two lines can be parallel or not. The angles formed are called corresponding angles and alternate angles.
Parallel lines are those which never intersect each other even when extended to infinity.