Question

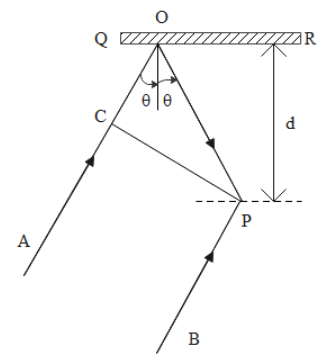
In the adjacent diagram, CP represents a wave front and AO and BP. The corresponding two rays. Find the condition on $\theta $ for constructive interference at P between the ray BP and the reflected ray OP.

Answer 1

Hint: For the constructive interference to take place, the path difference between two interfering waves should be half integral multiple of the wavelength of the light. Using the given diagram and rules of trigonometry, we can derive the required condition on $\theta $ for constructive interference at P between the ray BP and the reflected ray OP.

Complete answer:
We are given a wave front CP. The ray AO is incident on a reflecting surface QR and the reflected ray OP meets the ray BP at point P. We need to find the condition on $\theta $ for constructive interference at P between the ray BP and the reflected ray OP.
From the diagram, we can find the following relations between various lengths.
$OP = d\sec \theta $
In the triangle COP, $CO = PO\cos 2\theta $
Inserting the value of OP, we get $CO = d\sec \theta \cos 2\theta $
Now we can write the path difference between the two rays of the wave front in the following way.
$\Delta = CO + PO = d\sec \theta + d\sec \theta \cos 2\theta $
In order to obtain the constructive interference, the value of path difference should be
$\Delta = \dfrac{\lambda }{2},\dfrac{{3\lambda }}{2},\dfrac{{5\lambda }}{2},...$
For the first order maximum, we can write
$
 \Rightarrow d\sec \theta + d\sec \theta \cos 2\theta = \dfrac{\lambda }{2} \\
\Rightarrow d\sec \theta \left( {1 + \cos 2\theta } \right) = \dfrac{\lambda }{2} \\
\Rightarrow d\sec \theta \times 2{\cos ^2}\theta = \dfrac{\lambda }{2} \\
\Rightarrow 2d\cos \theta = \dfrac{\lambda }{2} \\
\Rightarrow \theta = {\cos ^{ - 1}}\left( {\dfrac{\lambda }{{4d}}} \right) \\
 $
This is the required condition on $\theta $ for constructive interference at P between the ray BP and the reflected ray OP.

Note:
The given diagram helps us understand how we can obtain the interference from a single wave front. The reflection allows us to change the path of the light wave. The reflected waves interfere with the original wave from the wave front and give us an interference pattern. The angle that we have obtained is the value of theta at which we will obtain constructive interference at point P where the original ray and the reflected ray meet.