Question

In the adjacent diagram, CP represents a wavefront and AO and BP, the corresponding two rays. Find the condition on $\text{ }\!\!\theta\!\!\text{ }$ for constructive interference at P between the ray BP and reflected ray OP.

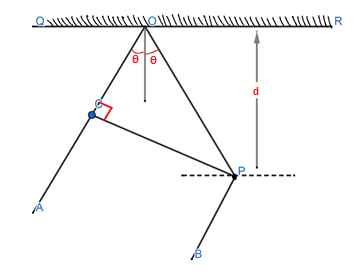
$\begin{align}
  & \text{A}\text{. }\cos \theta =\dfrac{3\lambda }{2d} \\
 & \text{B}\text{. }\cos \theta =\dfrac{\lambda }{4d} \\
 & \text{C}\text{. }\sec \theta -\cos \theta =\dfrac{\lambda }{d} \\
 & \text{D}\text{. }\sec \theta -\cos \theta =\dfrac{4\lambda }{d} \\
\end{align}$

Answer 1

Hint: The two light rays that are interfering at point P are the waves BP and OP. So OP is a part of the original wavefront AO and OP is the reflected part of the wavefront AO. A light undergoing a reflection suffers a phase change of ${{180}^{\circ }}\text{ or }\pi $. So, in order to create interference, the two waves interfering should be in phase. So, the path difference between these two waves should be an integral multiple of the wavelength.

Complete step-by-step answer:

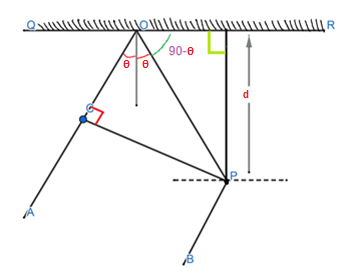
From the figure above we can understand that the ray OP had to travel an extra distance of CO and OP in order to reach point P. This extra distance is defined as the path difference between the two waves interfering at point P. Since there is a reflection taking place, there is an extra path difference of $\dfrac{\lambda }{2}$ between the two waves which are interfering.
So, the condition for interference, in this case, is that the total path difference should be an integral multiple of $\dfrac{\lambda }{2}$. So, we can write,
$\text{Total Path Difference}=n\dfrac{\lambda }{2}$
We know that the total path difference is the sum of distances CO and OP. So, we can write
$CO+OP=n\dfrac{\lambda }{2}$ … equation (1)
We can express OP as,
$\sin \left( {{90}^{\circ }}-\theta \right)=\dfrac{d}{OP}$
$\therefore OP=\dfrac{d}{\cos \theta }$ … equation (2)
After the value of OP, we can determine the value of CO as,
$\cos \left( 2\theta \right)=\dfrac{CO}{OP}\text{ }\left( \because \angle COP=2\theta \right)$
$\Rightarrow CO=OP\operatorname{Cos}\left( 2\theta \right)$
Substituting the value of OP from equation (1) into the equation above,
$\therefore CO=\dfrac{d\cos \left( 2\theta \right)}{\cos \theta }$ … equation (3)
Substituting the values from equation (2) and equation (3) in equation (1), we get,
$\dfrac{d}{\cos \theta }\cos \left( 2\theta \right)+\dfrac{d}{\cos \theta }=\dfrac{n\lambda }{2}$
$\dfrac{d}{\cos \theta }\left( 2{{\cos }^{2}}\theta -1 \right)+\dfrac{d}{\cos \theta }=\dfrac{n\lambda }{2}\text{ }\left( \because \cos 2\theta =2{{\cos }^{2}}\theta -1 \right)$
$\dfrac{d}{\cos \theta }\left( 2{{\cos }^{2}}\theta -1+1 \right)=\dfrac{n\lambda }{2}$
$\therefore 2d\cos \theta =\dfrac{n\lambda }{2}$

Let n=1, so, the condition for interference can be written as,
$\cos \theta =\dfrac{\lambda }{4d}$
So, the answer to the question is option (B).

Note: The condition for constructive interference for two light rays at a point P is given by the condition is given by, $\Delta x=n\lambda $, where$\lambda $ is the wavelength of light, $\Delta x$ is the path difference. This relation means that two waves produce a constructive interference if the path difference between them is an integral multiple of the wavelength of light.
The condition for destructive interference for two light rays at a point P is given by the condition is given by, $\Delta x=\left( 2n+1 \right)\dfrac{\lambda }{2}$, where$\lambda $ is the wavelength of light, $\Delta x$ is the path difference. This relation means that two waves produce a destructive interference if the path difference between them is an integral multiple of half the wavelength of light.