Question

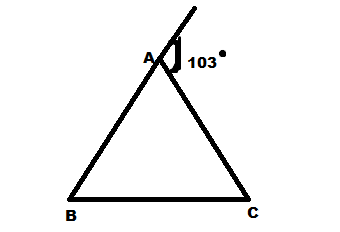
In the above diagram,$\angle B:\angle C = 2:3$ . Then $\angle B = {\left( {\dfrac{{206}}{5}} \right)^ \circ }$

a.True
b.False

Answer 1

Hint: We are given that $\angle B:\angle C = 2:3$and from this we get $\angle B = 2x{\text{ and }}\angle C = 3x$ and by using the property, exterior angle of a triangle is equal to the sum of the opposite interior angles, we get the value of x and using which we get the value of $\angle B$

Complete step-by-step answer:

We are given that $\angle B:\angle C = 2:3$
From this $\angle B = 2x{\text{ and }}\angle C = 3x$
Using the property, the exterior angle of a triangle is equal to the sum of the opposite interior angles.
$
   \Rightarrow \angle B + \angle C = {103^ \circ } \\
   \Rightarrow 2x + 3x = {103^ \circ } \\
   \Rightarrow 5x = {103^ \circ } \\
   \Rightarrow x = \dfrac{{{{103}^ \circ }}}{5} \\
$
And we have that $\angle B = 2x$
$
   \Rightarrow \angle B = 2*{\left( {\dfrac{{103}}{5}} \right)^ \circ } \\
   \Rightarrow \angle B = {\left( {\dfrac{{206}}{5}} \right)^ \circ } \\
$
Therefore the given statement is true .
The correct option is a.

Note: Triangle Sum Theorem - The sum of the 3 angles in a triangle is always 180°
The sum of an interior angle and its adjacent exterior angle is 180°
Exterior Angle Theorem - An exterior angle of a triangle is equal to the sum of the two opposite interior angles.
An equilateral triangle has 3 equal angles that are 60° each. An isosceles triangle has 2 equal angles, which are the angles opposite the 2 equal sides.