Question

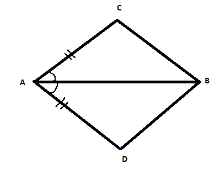
In quadrilateral \[ACBD\],$AB$ bisects $\angle A$ . Show that$\vartriangle ABC \cong \vartriangle ABD$.

Answer 1

Hint: In this problem we are going to prove that two triangles are congruent.
Let observe the sides and angles of the triangle.
Then, we have a check rule of congruence.
And apply the rule for the triangles $\vartriangle ABC$ and $\vartriangle ABD$
Finally we get the required answer.
SAS (Side-Angle-Side) rule: If two sides and the included angle of a triangle are equal to the two sides and included angle of the other triangle. Then, the two triangles are congruent.

Complete step-by-step answer:
Given: In quadrilateral \[ACBD\],
We have the two side of the triangle are equal, \[AC = AD\]
Since, we have line segment $AB$ bisects $\angle A$
Then to prove that $\vartriangle ABC \cong \vartriangle ABD$
Consider the two triangles, $\vartriangle ABC$ and $\vartriangle ABD$
The side $AB$ is common for two triangles
And we have sides $AC$ and $AD$ are equal.
That is, $AB$=$AB$& \[AC = AD\]
Here the line segment $AB$ bisector of $\angle A$.
Then, the$AB$ divides$\angle A$ into two equal parts
 Therefore, $\angle CAB = \angle DAB$
Now, we have to apply the SAS (Side-Angle-Side) rule for the triangles $\vartriangle ABC$ and $\vartriangle ABD$
Here, $AB$ is common for two triangles includes$AC$and $AD$are equal and $\angle CAB = \angle DAB$
Then the triangles $\vartriangle ABC$ and $\vartriangle ABD$ are congruent

Therefore, $\vartriangle ABC \cong \vartriangle ABD$

Note: Two triangles are congruent if sides and angles of a triangle are equal to the respective sides and angles of the other triangle.
An angle bisector divides the angle into two angles with equal measures. An angle has only one bisector.
Congruent angles have the same angle but don’t need to have to point in same direction and don’t have to be on similar sized lines.