Question

In process $ 2 $ , energy dissipated across the resistance $ {E_D} $ is

 $ \left( A \right){E_D} = 3\left( {\dfrac{1}{2}C{V_0}^2} \right) \\
  \left( B \right){E_D} = \dfrac{1}{2}C{V_0}^2 \\
  \left( C \right){E_D} = 3C{V_0}^2 \\
  \left( D \right){E_D} = \dfrac{1}{3}\left( {\dfrac{1}{2}C{V_0}^2} \right) \\ $

Answer 1

Hint :In order to solve this question, we need to analyze the two processes as given in the question, then, the dissipation energy of the charged capacitor $ {E_D} $ is calculated by subtracting the voltage change from the work done for charging the capacitor, the difference gives us the correct value of $ {E_D} $ .
Formula used: The formula for the dissipation energy of a charged capacitor is:
 $ {E_D} = {W_b} - \Delta V $
Where, work done is given by
 $ {W_b} = \dfrac{{C{V_0}}}{3}\left( {\dfrac{{{V_0}}}{3} + \dfrac{{2{V_0}}}{3} + {V_0}} \right) $
And voltage change by
 $ \Delta V = \dfrac{1}{2}C{V_0}^2 $

Complete Step By Step Answer:
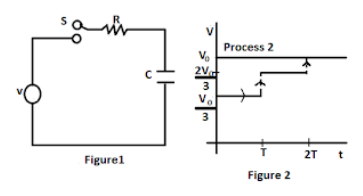
Consider a simple RC circuit as shown in figure $ 1 $
In the process $ 2 $ ,as we can see in the figure $ 2 $ the voltage is first decreased to one third of the voltage $ {V_0} $ , i.e. $ \dfrac{{{V_0}}}{3} $ and kept at that value for time $ T > > RC $ , then the voltage is increased to twice this voltage , i.e. $ \dfrac{{2{V_0}}}{3} $ and again kept at the same for time $ T > > RC $ . Then, this process is repeated again and the voltage is increased to the value $ {V_0} $ .
Now the dissipation energy for the capacitor is $ {E_D} $ and its value is calculated as
 $ {E_D} = {W_b} - \Delta V \\
   \Rightarrow {E_D} = \dfrac{{C{V_0}}}{3}\left( {\dfrac{{{V_0}}}{3} + \dfrac{{2{V_0}}}{3} + {V_0}} \right) - \dfrac{1}{2}C{V_0}^2 \\
   \Rightarrow {E_D} = \dfrac{{C{V_0}}}{3}\left( {2{V_0}} \right) - \dfrac{1}{2}C{V_0}^2 = \dfrac{{C{V_0}^2}}{6} \\ $
This is the same energy value as given in the option $ \left( D \right){E_D} = \dfrac{1}{3}\left( {\dfrac{1}{2}C{V_0}^2} \right) $ , hence, $ \left( D \right) $ is correct. $ {V_0} $

Note :
In the Process $ 1 $ , as we can see in the circuit, the switch S is closed here at $ t = 0 $ and the capacitor has the full charge with the voltage. For the time, $ T > > RC $ , the capacitor continues to charge . Across the resistance $ R $ , the dissipation that occurs is $ {E_D} $ . The energy stored in the fully charged capacitor is finally $ {E_C} $ .