Question

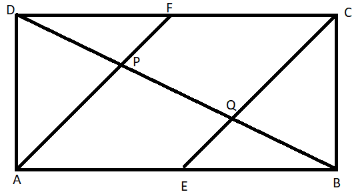
In parallelogram ABCD, E and F are midpoints of AB and DC respectively.
To prove: AF and EC trisect diagonal BD.

Answer 1

Hint: In the question we are asked to prove that AF and EC trisect diagonal BD. Trisect means dividing into 3 equal parts.
SO we have to show that DP = PQ = QB. We can use the concept that parallelograms with either pair of opposite sides are equal and parallel.
Apply converse of mid-point theorem.

Complete step-by-step answer:
It is given in the problem that ABCD is parallelograms and E and F are mid-points of AB and CD respectively.
We have to show that AF and EC trisect the diagonal BD. That is, DP = PQ = QB.
As ABCD is a parallelogram, then use the property of parallelogram to get:
\[AB\parallel CD \Rightarrow AE\parallel FC\] (As AE is the part of AB and FC is the part of CD)
\[AB = CD\] (As opposite sides of the parallelogram are equal and parallel)
\[ \Rightarrow \dfrac{1}{2}AB = \dfrac{1}{2}CD\]
\[ \Rightarrow AE = FC\] (E and F are mid-points of AB and CD respectively)
\[AE\parallel FC\] and \[AE = FC\]
So, AECF is a parallelogram. (If pair of opposite sides of a quadrilateral is equal and parallel, then it is a parallelogram)
Since AECF is a parallelogram and obtained the result.
\[AF\parallel EC\].
In \[\Delta DCQ\],
\[PF\parallel QC\] (As\[AF\parallel EC\])
As, F is mid-point of DC and \[PF\parallel QC\], then by the converse of mid-point theorem,
P is the mid-point of DQ.
\[ \Rightarrow DP = PQ\] … (1)
Now, in \[\Delta ABP\]
\[EQ\parallel AP\] (As, \[AF\parallel EC\])
As, E is midpoint of AB and \[EQ\parallel AP\], then by the converse of mid-point theorem
Q is the mid-point of BP
\[ \Rightarrow BQ = PQ\] … (2)
From equation (1) and (2)
\[DP = PQ = BQ\]
So we proved that $DP = PQ = BQ$.
Thus, AF and EC trisect the diagonal BD.

Note: The converse midpoint theorem states that if a line is drawn through the midpoint of a side of a triangle parallel to the second side, it will bisect the third side.