Question

In graphical representation of \[y=-4\] , line is:
A. Parallel to X-axis
B. Parallel to Y-axis
C. Passes through the origin
D. None of these.

Answer 1

Hint: To find the nature of the line \[y=-4\] , we should first draw the graph of this. Here, the coordinate of x is zero. Since the value of y is negative, the line falls below the X-axis. If it is positive, it will fall above the X-axis. From the graph, we can observe the true option.

Complete step-by-step solution
We need to find the nature of the line \[y=-4\]. For this, let us draw the line on the graph.
In the equation \[y=-4\], we know that the value of x coordinate will be zero always.

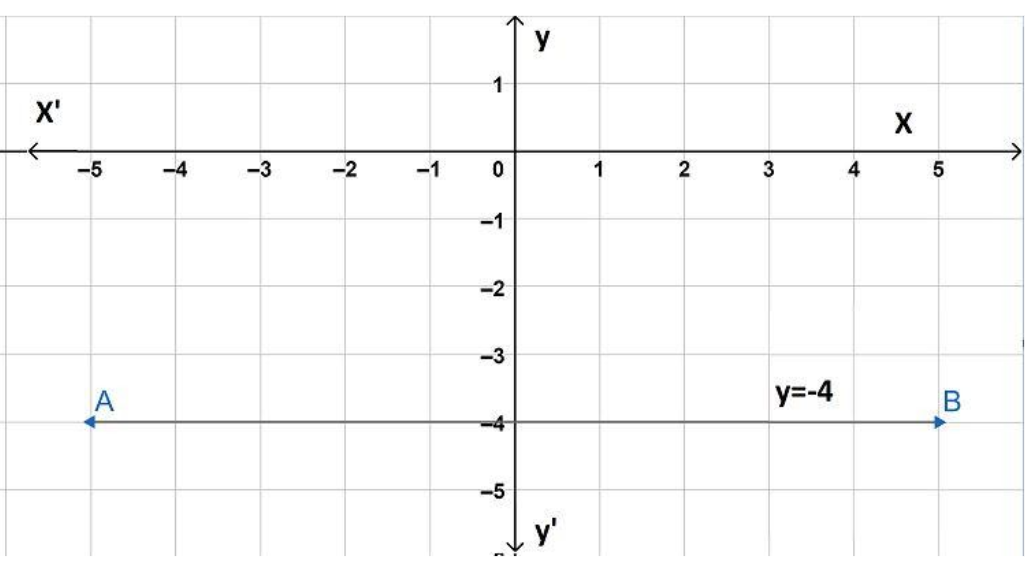
We can also observe that the value of y is negative. Hence, \[y=-4\] falls below the X-axis. If it was positive, the line would fall above the X-axis. We can see from the figure that \[y=-4\] will be parallel to the x-axis.
In general, any line for which $x$ coordinate is zero, that is for lines $y=a\text{ or }y=-a$, where ‘a’ is a constant, that line will be always parallel to X-axis.
Hence, option A is true.
Now, let us consider option B. It is clear that the line \[y=-4\] is never parallel to the Y-axis. Hence, option B is false.
Let us consider option C. Clearly, from the graph, \[y=-4\] is never passed through the origin.
Hence, the correct option is A.

Note: In lines with one zero coordinate, for example, $y=\pm a\text{ and }x=\pm a$ , where a is a constant, these lines will be parallel to X-axis and Y-axis respectively. For a line to lie on the origin, both the x and y coordinated must be 0.