Question

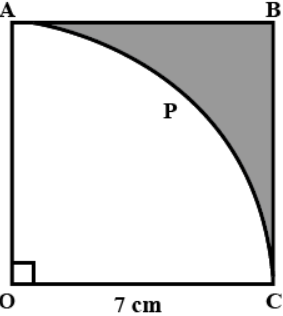
In given figure, OABC is square of side 7 cm. If OAPC is a quadrant of a circle with centre O, then find the area of the shaded region. \[\left( {use\,\,\pi = \dfrac{{22}}{7}} \right)\]
                                                             

Answer 1

Hint: Here in this question, we have to find the area of the shaded portion in the given figure. For finding this firstly, we have to find the area of the square OABC using the Area of square formula \[A = {\left( {side} \right)^2}\] and find the area of sector OAPC using the formula of area of sector\[ = \dfrac{\theta }{{{{360}^ \circ }}}\pi {r^2}\] later we have to find the area of shaded portion by subtracting the area of sector OAPC in Area of square OABC we get the required solution.

Complete step by step answer:
Area of a square is defined as the number of square units needed to fill a square. In general, the area is defined as the region occupied inside the boundary of a flat object or 2d figure. The measurement is done in square units with the standard unit being square meters (m2).
Therefore, the area of square = \[{\left( {side} \right)^2}\] square units.
The area of a sector is the region enclosed by the two radii of a circle and the arc. In simple words, the area of a sector is a fraction of the area of the circle.
Therefore, the area of sector = \[\dfrac{\theta }{{{{360}^ \circ }}}\pi {r^2}\].
Consider the OABC is square of side 7 cm
The area of square OABC is
 \[ \Rightarrow {\left( 7 \right)^2}\,\,c{m^2}\]
\[ \Rightarrow \,49\,\,c{m^2}\]
And, the OAPC is a quadrant of a circle with centre O.
The area of sector OAPC is
Here, radius of sector \[r = 7\,\,cm\] and \[\theta = {90^0}\] (\[\because \] in square all angles are equal to \[{90^0}\]) and given \[\pi = \dfrac{{22}}{7}\], then
\[ \Rightarrow \,\,\dfrac{{{{90}^ \circ }}}{{{{360}^ \circ }}} \times \dfrac{{22}}{7} \times {7^2}\,\,c{m^2}\]
 \[ \Rightarrow \,\,\dfrac{1}{4} \times 22 \times 7\,\,c{m^2}\]
\[ \Rightarrow \,\,\dfrac{1}{4} \times 154\,\,c{m^2}\]
\[ \Rightarrow \,\,38.5\,\,c{m^2}\]
Now, find the area of the shade portion is
\[ \Rightarrow \;{\text{ }}Area{\text{ }}of{\text{ }}shaded{\text{ }}region{\text{ }} = {\text{ }}Area{\text{ }}of{\text{ }}square\;OABC\; - {\text{ }}Area{\text{ }}of{\text{ }}sector\;OAPC\]
\[ \Rightarrow \,\,\left( {49 - 38.5} \right)\,\,c{m^2}\]
\[ \Rightarrow \,\,10.5\,\,c{m^2}\]

Hence, the area of shaded region is the given figure is \[10.5\,\,c{m^2}\].

Note: Here in this question, we are finding the area of the shaded region, to find that we must know the formula of an area of a square and the formula of area of sector. While simplifying this we use the simple arithmetic operations. We should also write the unit in the last place. We should not miss that.