Question

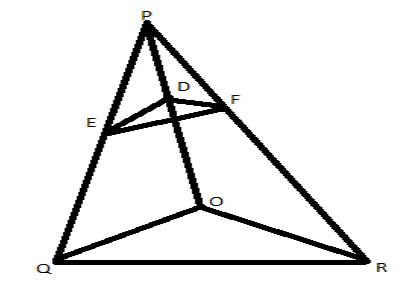
In figure, \[DE\parallel OQ\] and \[DF\parallel OR\]. Show that \[EF\parallel QR\].

Answer 1

Hint: To solve this geometry, use a similar triangle concept. Similar triangles, two figures having the same shape (but not necessarily the same size) are called similar figures.
The first part of the solution is important, for that, we use one of the theorems of a similar triangle that is, if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
The second part of the solution is done by using “if a line divides any two sides of a triangle in the same ratio, the line is parallel to the third side”.

Complete step-by-step answer:
Given: \[DE\parallel OQ\] and \[DF\parallel OR\]
To show that: \[EF\parallel QR\]
In \[\Delta PQO\],
\[DE\parallel OQ\]
Here, by the theorem, in a \[\Delta PQO\] the line \[DE\]which is parallel to \[OQ\] intersects the other two sides in distinct points, so it divides the other two side in same ratio
 The ratio is, \[\dfrac{{PE}}{{EQ}} = \dfrac{{PD}}{{DO}}...\left( 1 \right)\]
Similarly,
In \[\Delta PRO\],
\[DF\parallel OR\]
Here, by the theorem, in a \[\Delta PRO\] the line \[DF\]which is parallel to \[OR\] intersects the other two sides in distinct points, so it divides the other two side in same ratio
The ratio is, \[\dfrac{{PF}}{{FR}} = \dfrac{{PD}}{{DO}}...\left( 2 \right)\]
The ratio of \[(1)\ & (2)\]shows the two \[\Delta PRO\] and \[\Delta PQO\], \[\angle PQO = \angle PRO\] also corresponding sides are same ratio\[\dfrac{{PE}}{{EQ}} = \dfrac{{PD}}{{DO}}\]=\[\dfrac{{PF}}{{FR}} = \dfrac{{PD}}{{DO}}\]
Thus,\[\dfrac{{PE}}{{EQ}} = \dfrac{{PF}}{{FR}}\]
Now, we can say that the triangle is a similar triangle.
To show that the side is parallel, we use the second part of the hint
In a \[\Delta PQR\],
Line \[EF\]divides the \[\Delta PQR\] in the same ratio, therefore
\[EF\parallel QR\]
Hence proved.

Note: The theorem, we state the first part and second part is called basic proportionality theorem.
Two triangles are said to be similar, if their corresponding angles are equal and their corresponding sides are in the same ratio proportion.