Question

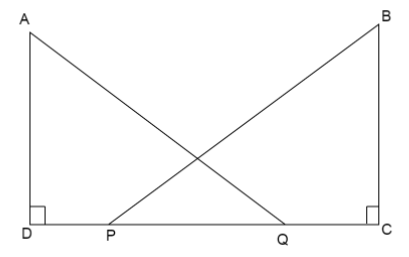
In figure, \[AD \bot CD,BC \bot CD\]. If \[AQ = BP,DP = CQ\] then prove that \[\angle DAQ = \angle CBP\]

Answer 1

Hint:Here we prove the two right angled triangles congruent by Side angle side congruence and since we know corresponding angles of congruent triangles are equal which will give us our required proof.
* Two triangles are congruent if they follow any of the following associativity
SAS – Side, angle, side
SSS – Side, Side, Side
AAA – Angle, Angle, Angle
* Perpendicular at any point of the line makes a right angle at that point.

Complete step-by-step answer:
We are given that \[AD \bot CD,BC \bot CD\] and since we know that if two line segments are perpendicular to each other at a point means they form \[{90^ \circ }\] angle at that point.
So, \[\angle ADQ = \angle ACP = {90^ \circ }\]
Also, we have \[AQ = BP\]
We have \[DP = CQ\]
Now we know if we add the same quantity to both sides of the equation then the equality remains unchanged.
Therefore, adding the length \[PQ\] on both sides of the equation
\[DP + PQ = CQ + PQ\]
From the figure, the length \[DP + PQ = DQ,CQ + PQ = CP\] the equation becomes
\[DQ = CP\]
Now we prove the two triangles \[\vartriangle ADQ \cong \vartriangle BCP\]
We have \[DQ = CP\], \[AQ = BP\] and \[\angle ADQ = \angle ACP = {90^ \circ }\]
Therefore, we have two sides equal and one angle equal in both triangles. So, by SAS associativity
\[\vartriangle ADQ \cong \vartriangle BCP\].
Now from the property of congruent triangles, the corresponding angles are equal if two triangles are congruent to each other.
So here the set of corresponding angles equal are \[\angle DAQ,\angle CBP\]
Thus, \[\angle DAQ = \angle CBP\]

Note:Students are likely to make mistake while making out which angle is equal to which angle when two triangles are congruent, so use the fact that we move from left to right while writing the angles when we are given which triangle is congruent to which triangle.