
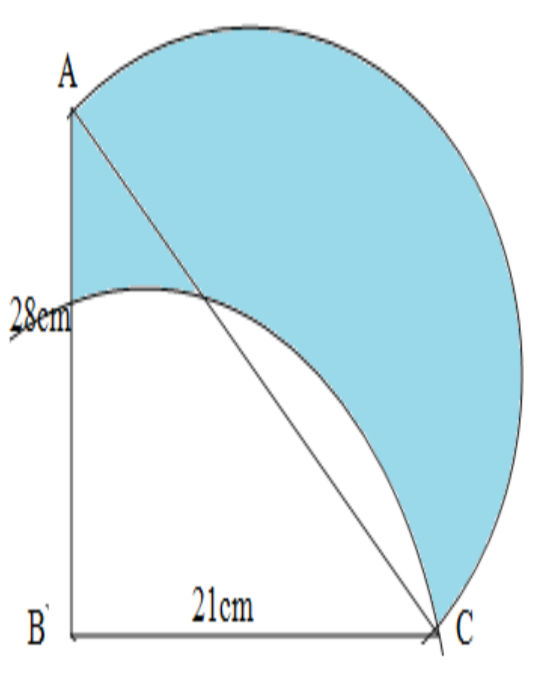
In figure ABC is a right angle triangle, $\angle B={{90}^{\circ }}$ AB=28cm and BC=21cm. With AC as a diameter a semicircle is drawn and BC as radius, a quarter circle is drawn. Find the area of the shaded region.

Answer
585.6k+ views
Hint: We find AC using Pythagoras theorem. We add the areas of the triangle say ${{A}_{t}}$ and the semi-circle say ${{A}_{s}}$ and then subtract the area of the quarter circle ${{A}_{q}}$ then we can get the required area enclosed by the semicircle and the quarter circle as $A={{A}_{t}}+{{A}_{s}}-{{A}_{q}}$
Complete step-by-step solution:
We are given in the figure a right-angled triangle ABC with $\angle B={{90}^{\circ }}$ AB=28cm and BC=21cm. A semicircle is drawn With AC as diameter and, a quarter circle is drawn. taking BC as the radius. We are asked to find the shaded area which is enclosed by the larger semi-circle which is drawn taking AC as diameter and the quarter circle taking BC as the radius. If we can add the areas of the triangle say ${{A}_{t}}$ and the semi-circle say ${{A}_{s}}$ and then subtract the area of the quarter circle ${{A}_{q}}$ then we can get the required result.
We know that area of a right-angled triangle is half of the product of sides adjacent to right angle which in this case are AB and BC. So the area of the triangle in square cm is,
\[{{A}_{t}}=\dfrac{1}{2}\times AB\times BC=\dfrac{1}{2}\times 21\times 28=294\]
We also know from Pythagoras theorem states that “ In a right-angled triangle the square of hypotenuse is sum of squares of other two sides.” AC is the hypotenuse as it is the side opposite to $\angle B={{90}^{\circ }}$. Now we have,
\[\begin{align}
& A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}={{21}^{2}}+{{28}^{2}} \\
& \Rightarrow A{{C}^{2}}=1225 \\
& \Rightarrow AC=\sqrt{1225}=35 \\
\end{align}\]
We know that the area of circle with radius $r$ is $\pi {{r}^{2}}$. The area of the semi-circle with diameter AC will be half of area of the circle. So the area with semi-circle with radius $\dfrac{AC}{2}$in square cm is
\[{{A}_{s}}=\dfrac{1}{2}\pi {{\left( \dfrac{AC}{2} \right)}^{2}}=\dfrac{1}{2}\pi {{\left( \dfrac{AC}{2} \right)}^{2}}=\dfrac{1}{2}\times 3.14\times {{\left( \dfrac{35}{2} \right)}^{2}}=480.8\]
The area of the quarter circle with radius BC will be one-fourth of area of the whole circle. So the area of the quarter circle in square cm is
\[{{A}_{q}}=\dfrac{1}{4}\pi {{\left( BC \right)}^{2}}=\dfrac{1}{4}\pi \times {{21}^{2}}=346.2\]
Now we can find the area of the shaded region $A$ in square cm as
\[A={{A}_{t}}+{{A}_{s}}-{{A}_{q}}=294+480.8-346.2=428.6 \]
Note: We have taken the value of $\pi $ as 3.14 and we can also use $\pi =\dfrac{22}{7}$ to find an approximate answer. We can also use the area of any sector of a circle which makes an angle $\theta $ at the center ${{A}_{\theta }}=\dfrac{\theta }{2}\times {{r}^{2}}$ to find the areas of semi-circle and quarter circle.
Complete step-by-step solution:

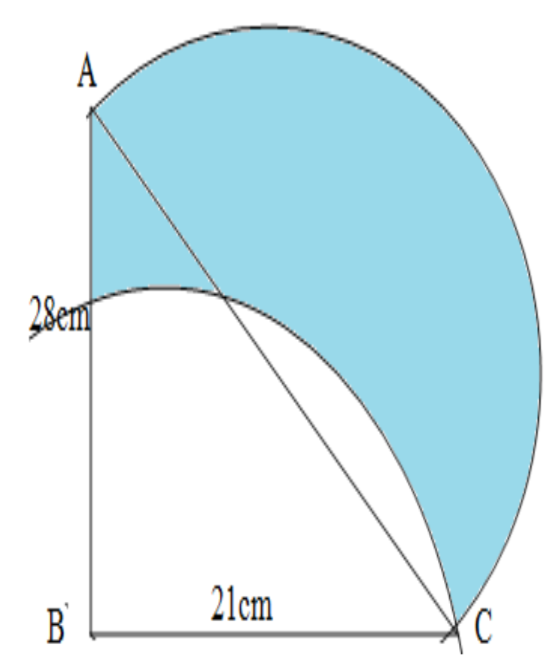
We are given in the figure a right-angled triangle ABC with $\angle B={{90}^{\circ }}$ AB=28cm and BC=21cm. A semicircle is drawn With AC as diameter and, a quarter circle is drawn. taking BC as the radius. We are asked to find the shaded area which is enclosed by the larger semi-circle which is drawn taking AC as diameter and the quarter circle taking BC as the radius. If we can add the areas of the triangle say ${{A}_{t}}$ and the semi-circle say ${{A}_{s}}$ and then subtract the area of the quarter circle ${{A}_{q}}$ then we can get the required result.
We know that area of a right-angled triangle is half of the product of sides adjacent to right angle which in this case are AB and BC. So the area of the triangle in square cm is,
\[{{A}_{t}}=\dfrac{1}{2}\times AB\times BC=\dfrac{1}{2}\times 21\times 28=294\]
We also know from Pythagoras theorem states that “ In a right-angled triangle the square of hypotenuse is sum of squares of other two sides.” AC is the hypotenuse as it is the side opposite to $\angle B={{90}^{\circ }}$. Now we have,
\[\begin{align}
& A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}={{21}^{2}}+{{28}^{2}} \\
& \Rightarrow A{{C}^{2}}=1225 \\
& \Rightarrow AC=\sqrt{1225}=35 \\
\end{align}\]
We know that the area of circle with radius $r$ is $\pi {{r}^{2}}$. The area of the semi-circle with diameter AC will be half of area of the circle. So the area with semi-circle with radius $\dfrac{AC}{2}$in square cm is
\[{{A}_{s}}=\dfrac{1}{2}\pi {{\left( \dfrac{AC}{2} \right)}^{2}}=\dfrac{1}{2}\pi {{\left( \dfrac{AC}{2} \right)}^{2}}=\dfrac{1}{2}\times 3.14\times {{\left( \dfrac{35}{2} \right)}^{2}}=480.8\]
The area of the quarter circle with radius BC will be one-fourth of area of the whole circle. So the area of the quarter circle in square cm is
\[{{A}_{q}}=\dfrac{1}{4}\pi {{\left( BC \right)}^{2}}=\dfrac{1}{4}\pi \times {{21}^{2}}=346.2\]
Now we can find the area of the shaded region $A$ in square cm as
\[A={{A}_{t}}+{{A}_{s}}-{{A}_{q}}=294+480.8-346.2=428.6 \]
Note: We have taken the value of $\pi $ as 3.14 and we can also use $\pi =\dfrac{22}{7}$ to find an approximate answer. We can also use the area of any sector of a circle which makes an angle $\theta $ at the center ${{A}_{\theta }}=\dfrac{\theta }{2}\times {{r}^{2}}$ to find the areas of semi-circle and quarter circle.
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

What are the major means of transport Explain each class 12 social science CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

Why cannot DNA pass through cell membranes class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

Draw a neat and well labeled diagram of TS of ovary class 12 biology CBSE




