Question

In figure, a regular hexagon of side length 5 cm is inscribed in a circle. Calculate the percentage of the circle that is shaded to the nearest tenth.

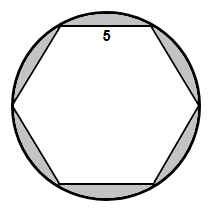
 (a) 13.6 %
(b) 17. 3 %
(c) 78.5 %
(d) 82.7 %
(e) 86.4 %

Answer 1

Hint: Name the hexagon as ABCDEF and its centre that will overlap with the centre of the circle as O. Join the points to form the lines OA and OB and assume the angle AOB = $\theta $. Find the value of $\theta $ by dividing ${{360}^{\circ }}$ into 6 parts and consider the triangle OAB as an equilateral triangle. Find the radius (r) of the circle and use the formula area of a circle = $\pi {{r}^{2}}$. To find the area of the hexagon, find the area of the equilateral triangle OAB by using the formula $\dfrac{\sqrt{3}}{4}\left( {{a}^{2}} \right)$, where a is the side of the triangle, and multiply it with 6. Finally, find the area of the shaded part by subtracting the area of the hexagon from the area of the circle. Take the ratio of this difference and the area of the circle and multiply it with 100 to get the answer.

Complete step by step answer:
Here we have been provided with the figure of a regular hexagon inscribed in a circle and we are asked to find the percentage of the circle that is shaded. Let us use some constructions to find the radius of the circle.

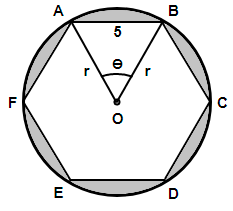
Now, in the above figure we have named the hexagon as ABCDEF and considered a point O at its center. Since the hexagon is regular and the vertices are touching the circle therefore the centre of the circle will overlap with O. Further we have joined the points to form the lines OA and OB.
The angle AOB is the central angle formed by one of the sides of the hexagon and we know that all the sides will subtend the same angle at the centre, so the complete central angle which is equal to ${{360}^{\circ }}$ will be divided into 6 equal parts, so we get,
\[\begin{align}
  & \Rightarrow \theta =\dfrac{{{360}^{\circ }}}{6} \\
 & \Rightarrow \theta ={{60}^{\circ }} \\
\end{align}\]
The lines OA and OB are the two radii of the circle so we have OA = OB = r and therefore the angle OAB = angle OBA. Since $\theta ={{60}^{\circ }}$ so using the angle sum property of the triangle we get,
$\begin{align}
  & \Rightarrow \angle OAB+\angle OBA+{{60}^{\circ }}={{180}^{\circ }} \\
 & \Rightarrow 2\angle OAB={{120}^{\circ }} \\
 & \Rightarrow \angle OAB=\angle OBA={{60}^{\circ }} \\
\end{align}$
That clearly means the triangle OAB is an equilateral triangle because all its angles measure ${{60}^{\circ }}$. Therefore all the sides of this triangle will be equal and hence we get r = 5 cm. Using the formula of the area of a circle given as $\pi {{r}^{2}}$ we get,
$\Rightarrow $ Area of the circle = $\pi \times {{5}^{2}}$
$\Rightarrow $ Area of the circle = $25\pi $ …….… (1)
Now, the area of the equilateral triangle OAB is given as $\dfrac{\sqrt{3}}{4}\left( {{a}^{2}} \right)$, where a (= r) is the side of the triangle, so we get,
$\Rightarrow $ Area of the triangle OAB = $\dfrac{\sqrt{3}}{4}\times {{5}^{2}}$
$\Rightarrow $ Area of the triangle OAB = $\dfrac{25\sqrt{3}}{4}$
Since, there will be 6 such triangles that are combined to form the regular hexagon, so we get,
$\Rightarrow $ Area of the hexagon ABCDEF = $\dfrac{25\sqrt{3}}{4}\times 6$
$\Rightarrow $ Area of the hexagon ABCDEF = \[\dfrac{75\sqrt{3}}{2}\] ……….. (2)
Therefore the total area of the shaded part = Area of the circle – Area of the hexagon
$\Rightarrow $ The total area of the shaded part = $\left( 25\pi -\dfrac{75\sqrt{3}}{2} \right)$
$\Rightarrow $ The percentage of the circle that is shaded = $\dfrac{\left( 25\pi -\dfrac{75\sqrt{3}}{2} \right)}{\left( 25\pi \right)}\times 100$%
Substituting the values $\pi =3.14$ and $\sqrt{3}=1.732$ we get,
$\Rightarrow $ The percentage of the circle that is shaded = 17.26 %
$\therefore $ The percentage of the circle that is shaded = 17.3 %
So, the correct answer is “Option b”.

Note: Note that we generally don’t remember any direct formula for the area of a regular hexagon and that is why we need to divide it into 6 equal triangles. You can also use the cosine rule to get the value of r so it must be remembered along with the sine rule. In the case of figures like pentagons inscribed in a circle we need the sine and the cosine rule because their equilateral triangles are not formed.