Question

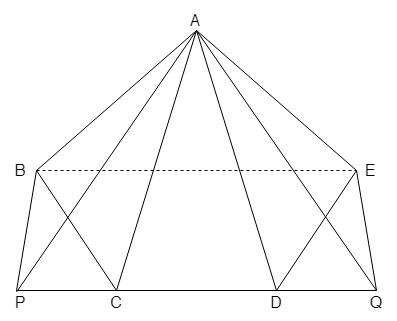
In Fig. ABCDE is any pentagon. BP drawn parallel to AC meets DC produced at P and EQ drawn parallel to AD meets CD produced at Q. Prove that ar (ABCDE) = ar (\[\Delta \]APQ).

Answer 1

Hint: According to the given question, we have to take two triangles that is \[\Delta ADQ\] , \[\Delta ADE\] and\[\Delta ACP\], \[\Delta ACB\] . Using these triangles we will prove that their areas are equal.

Complete step-by-step answer:
Given Points:
1.ABCDE is a pentagon
2.BP \[||\] AC
3.EQ \[||\] CD
We have to prove that ar (ABCDE) = ar (APO). Where ar stands for area.
So, let’s say that \[\Delta ADQ\] and \[\Delta ADE\] are at the same base that is AD and between the same parallel lines.
Therefore, we can say that their areas are equal, that is ar (\[\Delta \]ADQ) = ar (\[\Delta \]ADE). --Equation 1
So, let’s say that \[\Delta ACP\] and \[\Delta ACB\] are at the same base that is AC and between the same parallel lines.
Therefore, we can say that their areas are equal, that is ar (\[\Delta \]ACP) = ar (\[\Delta \]ACB). ---Equation 2
Using both the equations 1 and 2, by adding we get,
ar (\[\Delta \]ADQ) + ar (\[\Delta \]ACP) = ar (\[\Delta \]ADE) + ar (\[\Delta \]ACB)
As to make ar (\[\Delta \]APQ) on the left side and ar (ABCDE) on right side we must add ar (\[\Delta \]ACD) on both sides of the equation.
Hence, on adding we get,
ar (\[\Delta \]ADQ) + ar (\[\Delta \]ACP) + (\[\Delta \]ACD) = ar (\[\Delta \]ADE) + ar (\[\Delta \]ACB) + (\[\Delta \]ACD)
Therefore, ar (\[\Delta \]APQ) = ar (ABCDE)
Hence Proved

Note: To solve these types of questions, we need to proceed with the given points. Using the different properties of triangles we can calculate any type of requirement in the question.