Question

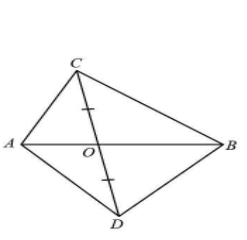
In fig, ABC and ABD are two triangles on the same base AB. If line segment CD is bisected by AB at O, show that \[ar\left( {ABC} \right) = ar\left( {ABD} \right)\].

Answer 1

Hint: Here, we will use a property of Median of a triangle. It says that median of a triangle divides the triangle in two triangles of equal area.


Complete Step-by-step Solution
Given- Line segment CD is bisected by AB at O. Therefore, \[CO = OD\].
We know that BO will be a median for triangle BCD and it will divide triangle BCD in two triangles of equal area.
\[ar\left( {BCO} \right) = ar\left( {BOD} \right)\]
Similarly, we can say that AO will be a median for triangle ACD and it will divide triangle ACD in two triangles of equal area.
\[ar\left( {AOC} \right) = ar\left( {ADO} \right)\]
On adding the above equations, we get the value,
\[\begin{array}{c}
ar\left( {BCO} \right) + ar\left( {AOC} \right) = ar\left( {BOD} \right) + ar\left( {ADO} \right)\\
ar\left( {ABC} \right) = ar\left( {ABD} \right)
\end{array}\]
Therefore, the required relation \[ar\left( {ABC} \right) = ar\left( {ABD} \right)\] is proved.

Note:Median of a triangle is a line segment that passes through one vertex and midpoint of the side opposite to that vertex. The median can divide the triangle in two smaller triangles and areas of both the triangles are the same.