Question

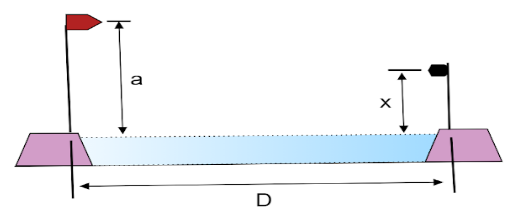
In Fig., a microwave transmitter at height $a$ above the water level of a wide lake transmits microwaves of wavelength $\lambda $ toward a receiver on the opposite shore, a distance $x$ above the water level. The microwaves reflecting from the water interfere with the microwaves arriving directly from the transmitter.

Assuming that the lake width $D$ is much greater than $a$ and $x$, and that $\lambda \geqslant a$, find an expression that gives the values of $x$ for which the signal at the receiver is maximum. (Hint: Does the reflection cause a phase change?)

Answer 1

Hint: Let us first talk about whether there is a phase change when a light reflects. Reflection of light causes a phase change only when the refractive index of the medium to which the light ray is falling has greater refractive index than the medium from which the light is coming.

Complete step by step answer:

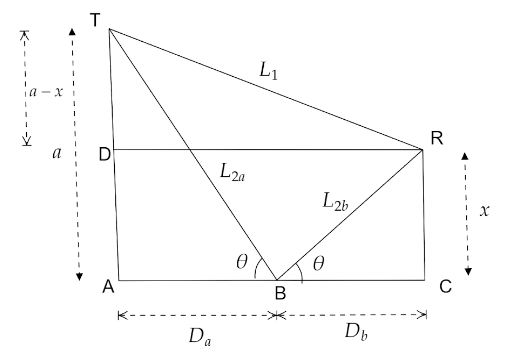
The given diagram has been drawn according to the statement from the question. Let ${L_1}$ be the distance covered by the wave directly while ${L_2}$ be the distance covered by the reflected wave. ${L_2}$ is again split up into two parts as ${L_{2a}}$ and ${L_{2b}}$.The wave suffers a phase change as the refractive index of water is more than air.As it suffers a phase change the wavelength also becomes half. In order to obtain a constructive interference at the receiver the path difference ${L_2} - {L_1}$ must be an odd multiple of half of the wavelength.

Now from right $\Delta $TAB we get,
$\tan \theta = \dfrac{a}{{{D_a}}}$
Hence we get,
${D_a} = \dfrac{a}{{\tan \theta }} - - - - \left( 1 \right)$
Again from right $\Delta $ RBC we get,
${D_b} = \dfrac{x}{{\tan \theta }} - - - - \left( 2 \right)$
Let $D = {D_a} + {D_b}$.
Therefore, $D = \dfrac{a}{{\tan \theta }} + \dfrac{x}{{\tan \theta }} = \dfrac{{a + x}}{{\tan \theta }}$
So, $\tan \theta = \dfrac{{a + x}}{D} - - - - \left( 2 \right)$
By using identity as,
${\sin ^2}\theta = \dfrac{{{{\tan }^2}\theta }}{{1 + {{\tan }^2}\theta }}$ we get,
$\Rightarrow \sin \theta = \dfrac{{\tan \theta }}{{\sqrt {1 + {{\tan }^2}\theta } }} - - - - - \left( 3 \right)$
Substituting the value of $\tan \theta $ from equation $\left( 2 \right)$ to equation $\left( 3 \right)$ we get,
$\sin \theta = \dfrac{{\dfrac{{a + x}}{D}}}{{\sqrt {1 + {{\left( {\dfrac{{a + x}}{D}} \right)}^2}} }}$

Arranging the equation we get,
$\sin \theta = \dfrac{{a + x}}{{\sqrt {{D^2} + {{\left( {a + x} \right)}^2}} }} - - - - \left( 4 \right)$
Now from right $\Delta $TAB we get,
${L_{2a}} = \dfrac{a}{{\sin \theta }}$
And from right $\Delta $ RBC we get, ${L_{2b}} = \dfrac{x}{{\sin \theta }}$
Now ${L_2} = {L_{2a}} + {L_{2b}} = \dfrac{{a + x}}{{\sin \theta }}$
Substituting the value of $\sin \theta $ from equation $\left( 4 \right)$ we get,
${L_2} = \dfrac{{a + x}}{{\dfrac{{a + x}}{{\sqrt {{D^2} + {{\left( {a + x} \right)}^2}} }}}} = \sqrt {{D^2} + {{\left( {a + x} \right)}^2}} $
As ${D^2} \gg {\left( {a + x} \right)^2}$ then by using binomial theorem we get,
${L_2} \approx D + \dfrac{{{{\left( {a + x} \right)}^2}}}{{2D}}$

From right $\Delta $TDR we get, ${L_1} = \sqrt {{D^2} + {{\left( {a - x} \right)}^2}} $ by Pythagoras theorem,
As ${D^2} \gg {\left( {a - x} \right)^2}$ then by using binomial theorem we get,
${L_1} \approx D + \dfrac{{{{\left( {a - x} \right)}^2}}}{{2D}}$
Let the path difference be $x$.
$x = {L_2} - {L_1}$
Substituting the values of ${L_1}$ and ${L_2}$ we get,
$x = D + \dfrac{{{{\left( {a - x} \right)}^2}}}{{2D}} - \left\{ {D + \dfrac{{{{\left( {a + x} \right)}^2}}}{{2D}}} \right\} \\
\Rightarrow x= \dfrac{{{{\left( {a + x} \right)}^2} - {{\left( {a - x} \right)}^2}}}{{2D}} \\
\Rightarrow x= \dfrac{{4ax}}{{2D}} \\
\Rightarrow x = \dfrac{{2ax}}{D} - - - - - - \left( 5 \right)$
The path difference for a constructive interference is,
$x = \left( {n + \dfrac{1}{2}} \right)\lambda - - - - - - \left( 6 \right)$ where $n = 0,1,2,...$
Comparing equation $\left( 5 \right)$ and $\left( 6 \right)$we get,
$\therefore \dfrac{{2ax}}{D} = \left( {n + \dfrac{1}{2}} \right)\lambda $

Therefore, $x = \dfrac{{D\lambda }}{{2a}}\left( {n + \dfrac{1}{2}} \right)$.

Note: It must be noted that reflection of light causes phase change only when the reflecting surface has a greater refractive medium. The phase change is ${180^ \circ }$. Say, a light travelling from air to water will have a phase change as the refractive index of water is more than war, but if the light ray is travelling from water to air, then there is no phase change as the refractive index of air is less than water.