Question

In fig. $10.10$ if \[AOB\] is a diameter and $\angle ADC = {120^0}$, then $\angle CAB = {30^0}$.
State true or false.

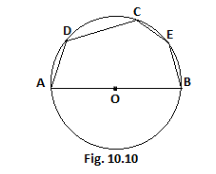
Answer 1

Hint: In the given question, we have to check whether $\angle CAB$ is equal to ${30^0}$ or not. To solve this question, we have to use some Geometric theorems, regarding cyclic quadrilateral, Angle of circle, chord of circles and tangents of circle. Since $\angle ADC$ is given, first join $A,C$ and $B,C$. Find out the value of $\angle CBA$ as $ADCB$ is a cyclic quadrilateral. Afterwards find out the $\angle CAD$ as $\angle ACB$ is angle on semicircle.

Complete step-by-step answer:

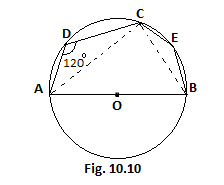
According to the hint,
Join $A,C$ and $B,C$.
In cyclic quadrilateral, $ADCB$-
We know, opposite angles of cyclic quadrilateral are supplementary.
$\therefore \angle ADC + \angle CBA = {180^0}$
&$\angle ADC = {120^0}$(given in question)
$\therefore \angle CBA = {180^0} - \angle ADC = {180^0} - {120^0}$
$\therefore $$\angle CBA = {60^0}$
In $\Delta ACB$-
$AOB$is a diameter.
$\therefore $$\angle ACB$is angle on semicircle & we know, angle one semicircle is right angle.
$\therefore \angle ACB = {90^0}$
Now, we get, $\angle ABC = {60^0}$
We know that the sum of all angles of a triangle is $180^\circ $.
$\therefore $In $\Delta AOB$-
${
  \therefore \angle ABC + \angle ACB + \angle CAB = {180^0} \\
   \Rightarrow {60^0} + {90^0} + \angle CAB = {180^0} \\
   \Rightarrow \angle CAB = {180^0} - {150^0} \\
  \therefore \angle CAB = {30^0} \\
} $[ Putting the values of known angles]

Hence, the given statement is true, $\angle CAB = {30^0}$.

Note: The terms used in the solution are important. Cyclic quadrilateral is the quadrilateral formed when all four vertices lie on circumference. We have learnt in ‘Angle of circle’ topic, that ‘Angles on the Centre are always double the angles on the circumference’, ‘Angles on the same segment are equal’, ‘Angles on semicircle are always ${90^0}$etc. The reason behind saying this is that, the asked question can also be solved using said theorems but the way using cyclic quadrilateral (as done) is much better and easy way to solve it.