Question

In \[\Delta {\text{PQR}}\] , right-angled at ${\text{Q}}$ , ${\text{PR}} + {\text{QR}} = 25{\text{cm}}$ and ${\text{PQ}} = {\text{5cm}}$. Determine the values of $\sin {\text{P}}$ , $\cos {\text{P}}$ and $\tan {\text{P}}$.

Answer 1

Hint: In this question first we will draw a triangle \[\Delta {\text{PQR}}\] having ${\text{Q}}$ as a right angle. Now we will find the length of ${\text{QR}}$ with the help of the equation given in the question and Pythagoras theorem. Now, with the help of ${\text{QR}}$ and ${\text{PR}}$. We will find what is asked in the question.

Complete step-by-step solution:
We know that ${\text{PQ}} = {\text{5}}\,cm$ (given in the question). Now we have to find the remaining sides of the triangle \[\Delta {\text{PQR}}\]

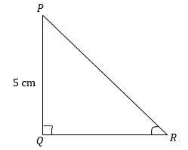
Now, we know that ${\text{PR}} + {\text{QR}} = 25$ (given in the question). Therefore, it can be written as ${\text{PR}} = 25 - {\text{QR}}$. From ${\text{PR}} = 25 - {\text{QR}}$we will find the length of ${\text{QR}}$.
From the figure we can write ${\text{P}}{{\text{R}}^{\text{2}}} = {\text{Q}}{{\text{R}}^{\text{2}}} + {\text{P}}{{\text{Q}}^{\text{2}}}\_\_\_(1)$
Put the values of ${\text{PQ}}$ and ${\text{PR}}$ in equation (1)
\[ \Rightarrow {\left( {{\text{25}} - {\text{QR}}} \right)^{\text{2}}} = {\text{Q}}{{\text{R}}^{\text{2}}} + {\left( {\text{5}} \right)^{\text{2}}}\]
Now, simplify the above equation
\[ \Rightarrow {\text{625}} - {\text{50QR}} + {\text{Q}}{{\text{R}}^{\text{2}}} = {\text{Q}}{{\text{R}}^{\text{2}}} + {\text{25}}\]
Now, cancel the common things
\[ \Rightarrow {\text{625}} - {\text{50QR}} - {\text{25}} = {\text{0}}\]
Now, we can easily find ${\text{QR}}$
$
   \Rightarrow 50{\text{QR}} = 600 \\
   \Rightarrow {\text{QR}} = 12
 $
Therefore, we found the length of ${\text{QR}}$ is $12{\text{cm}}$ . Now, we know that ${\text{PR}} = 25 - {\text{QR}}$.
$
  {\text{PR}} = 25 - {\text{QR}} \\
   \Rightarrow {\text{PR}} = 25 - 12 = 13
 $
From the above calculation we found the length of ${\text{PR}}$ is $13{\text{cm}}$.
Now, we know that $\sin {\text{P}} = \dfrac{{{\text{opposite side}}}}{{{\text{hypotenuse}}}}$ . From the figure we can write $\sin {\text{P}} = \dfrac{{{\text{QR}}}}{{{\text{PR}}}}$.
Therefore, we can write $\sin {\text{P}} = \dfrac{{{\text{QR}}}}{{{\text{PR}}}} = \dfrac{{12}}{{13}}$.
Similarly, we know that ${\text{cos P}} = \dfrac{{{\text{Adjacent side}}}}{{{\text{hypotenuse}}}}$ . From the figure we can write ${\text{cos P}} = \dfrac{{{\text{PQ}}}}{{{\text{PR}}}}$.
Therefore, we can write \[{\text{cos P}} = \dfrac{{{\text{PQ}}}}{{{\text{PR}}}} = \dfrac{5}{{13}}\].
Similarly, we know that ${\text{tan P}} = \dfrac{{{\text{opposite side}}}}{{{\text{Adjacent side}}}}$ . From the figure we can write ${\text{tan P}} = \dfrac{{{\text{QR}}}}{{{\text{PQ}}}}$.
Therefore, we can write \[{\text{tan P}} = \dfrac{{{\text{QR}}}}{{{\text{PQ}}}} = \dfrac{{12}}{5}\].

Hence, the answers are $\sin {\text{P}} = \dfrac{{12}}{{13}}$, \[{\text{cos P}} = \dfrac{5}{{13}}\] and \[{\text{tan P}} = \dfrac{{12}}{5}\].

Note: We can also solve this question by making ${\text{QR}}$ as a subject and then from it we can find ${\text{PR}}$ first. The other important things are the formula of $\sin $ , $\cos $ and $\tan $ which we need to memorize.
$\sin {\text{A = }}\dfrac{{{\text{Opposite}}}}{{{\text{Hypotenuse}}}}$
$\cos {\text{A = }}\dfrac{{{\text{Adjacent}}}}{{{\text{Hypotenuse}}}}$
$\tan {\text{A = }}\dfrac{{{\text{Opposite}}}}{{{\text{Adjacent}}}}$
$\cos ec {\text{A = }}\dfrac{{{\text{Hypotenuse}}}}{{{\text{Opposite}}}}$
$\sec {\text{A = }}\dfrac{{{\text{Hypotenuse}}}}{{{\text{Adjacent}}}}$
$\cot {\text{A = }}\dfrac{{{\text{Adjacent}}}}{{{\text{Opposite}}}}$