Question

In, $\Delta DEF,{\text{ if }}\angle {\text{D}} \equiv \angle {\text{F}}$ then
A. $DE \equiv EF \equiv DF$
B. $DE \equiv DF$
C. $DE \equiv EF$
D. All the above.

Answer 1

Hint: In this question, first we will make the diagram of the triangle, here given that two angles are equal to each other. So we will use the property that if in a triangle two opposite angles are equal then their corresponding sides will be equal to each other.

Complete step-by-step answer:

Given that in $\Delta DEF,{\text{ }}\angle {\text{D}} \equiv \angle {\text{F}}$

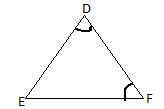
Here opposite sides of $\angle D$ and $\angle F$ are DE and EF.
We know that the angles opposite to equal sides in a triangle are equal. Similarly, the side opposite to equal angles is equal.
$\therefore \angle D = \angle F$
So, their opposite sides are also equal.

Hence, DE = DF and the correct answer is option “C”.

Note: In order to solve these types of questions, remember the basic properties of triangles and angles. In the above question we use the property of an isosceles triangle in which two sides of the triangle are equal and two angles are also equal. Similarly, remember the properties of the equilateral triangle and also remember that the sum of all angles of a triangle is 180 degree.