Question

In \[\Delta ABC\], \[m\angle B={{90}^{\circ }}\], \[\overline{BM}\bot \overline{AC}\], \[M\in AC\]. If \[AM-CM=7\]and \[A{{B}^{2}}-B{{C}^{2}}=175\], then find AC.

Answer 1

Hint: The line through M divides the \[\Delta ABC\] into two right angles triangles. By using the pythagoras theorem we will write this theorem for \[\Delta AMB\] and \[\Delta BMC\]. After writing the equations by substituting the term given in the question we get the solution.

Complete step-by-step answer:

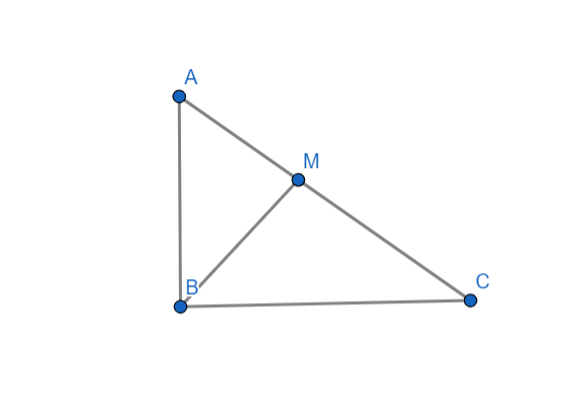
In \[\Delta AMB\]
\[A{{B}^{2}}=A{{M}^{2}}+B{{M}^{2}}\] . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (1)
In \[\Delta BMC\]
\[B{{C}^{2}}=C{{M}^{2}}+B{{M}^{2}}\] . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (2)
By doing (1) – (2) we get
\[A{{B}^{2}}\]- \[B{{C}^{2}}\]\[=A{{M}^{2}}+B{{M}^{2}}\]- (\[C{{M}^{2}}+B{{M}^{2}}\])
\[A{{B}^{2}}-~B{{C}^{2}}=A{{M}^{2}}+B{{M}^{2}}-~C{{M}^{2}}-B{{M}^{2}}\]
By cancelling the common terms we get \[A{{B}^{2}}-~B{{C}^{2}}=A{{M}^{2}}-C{{M}^{2}}\]
\[A{{B}^{2}}-~B{{C}^{2}}=\left( AM+CM \right)\left( AM-CM \right)\]
By substituting the values given in the question we get
\[175=\left( AM+CM \right)\left( 7 \right)\]
\[\left( AM+CM \right)=\dfrac{175}{7}=25\]
\[\left( AM+CM \right)\]= AC
AC = 25.
Therefore we have found the value of AC is 25.
Note: To solve this type of problem first we have to draw the figure. Pythagoras theorem should be used for two right angled triangles. Care should be taken while solving the equation. As we got two right angled triangles we have to use Pythagoras for sure.