Question

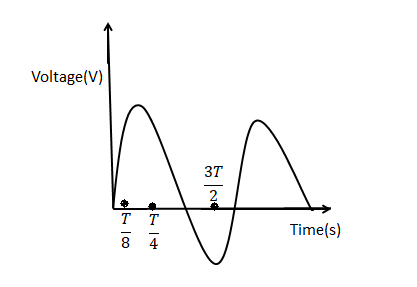
In an RL Series circuit, sinusoidal voltage \[v = {v_0}\;sin\;\omega t\] is applied. it is given that \[\dfrac{T}{2}\], \[R = 11\;\Omega \], \[{V_{rms}} = 220{\text{ V}}\], \[\dfrac{\omega }{{2\pi }}\; = 50{\text{ Hz}}\] and \[\pi = \dfrac{{22}}{7}\]. Obtain the phase difference between the current and voltage and find the amplitude of current in the steady state. Plot the variation of current for one cycle on the given graph.

Answer 1

Hint:A $LR$ Circuit consists of an inductor of inductance $L$ connected in series with a resistor of resistance $R$. First find the inductive reactance then find the maximum current flowing in the circuit. In the above waveform, time period is given as $2\pi $.Then from data obtained we can plot the variation of current for one cycle on the given graph.

Formula used:
\[{X_L} = \omega L\]
${I_{rms}} = \dfrac{{{V_{rms}}}}{{\sqrt {{R^2} + {X^2}} }}$
${I_{\max }} = {I_{rms}} \times \sqrt 2 $
Where ${X_L}$ is the inductive reactance, $R$ is the resistance, ${I_{\max }}$ is the maximum current,${I_{rms}}$ is the root mean square current.

Complete step by step answer:
$LR$ circuit consists of a resistor of resistance $R$ connected in series with an inductor $L$ .${V_R}$ is equal to $IR$ due to the voltage drop across the resistor. Hence it will have the same exponential shape and growth as the current. Just like $RC$ and $LCR$ circuit, RL circuit will also consume energy.
The current and voltage are in the same phase and the phase angle difference between current and voltage is zero, in case of resistors. The current and the voltage are not in phase. The current lags voltage by ${90^ \circ }$. As seen before the phase angle between voltage and current is zero in case of pure resistance circuit and phase angle${90^ \circ }$ in case of pure inductive circuit. But when we combine both resistance and inductor, $LR$ circuit phase angle is between ${0^ \circ }$to${90^ \circ }$.
\[{X_L} = \omega L\]$ = 2\pi \times 50 \times 35 \times {10^{ - 3}} = 11\Omega $
$\left( {1mH = 1 \times {{10}^{ - 3}}H} \right)$
${I_{rms}} = \dfrac{{{V_{rms}}}}{{\sqrt {{R^2} + {X^2}} }}$
${I_{rms}} = \dfrac{{220}}{{\sqrt {\left( {{{11}^2} + {{11}^2}} \right)} }} = $${I_{rms}} = \dfrac{{220}}{{\sqrt {\left( {{{11}^2} + {{11}^2}} \right)} }} = \dfrac{{20}}{{\sqrt 2 }}A$
Then the maximum current is given by
${I_{\max }} = {I_{rms}} \times \sqrt 2 = \dfrac{{20}}{{\sqrt 2 }} \times \sqrt 2 = 20A$
$\tan \phi = \dfrac{{{X_L}}}{R} = \dfrac{1}{1} = 1$
Therefore, the value of $\phi $ is $\dfrac{\pi }{4}$
Then the sinusoidal current equation is given by
$I = {I_{\max }}\sin \left( {\omega t + \phi } \right) = 20\sin \left( {\omega t + \dfrac{\pi }{4}} \right)$

Note:A $LR$ Circuit consists of an inductor of inductance $L$ connected in series with a resistor of resistance $R$. The impedance of $LR$ circuit opposes the flow of alternating current. The flow of alternating current opposed by the impedance of $LR$ circuit. $LR$ circuit phase angle is between ${0^ \circ }$ to ${90^ \circ }$. Just like $RC$ and $LCR$ circuit, $LR$ circuit will also consume energy.