Question

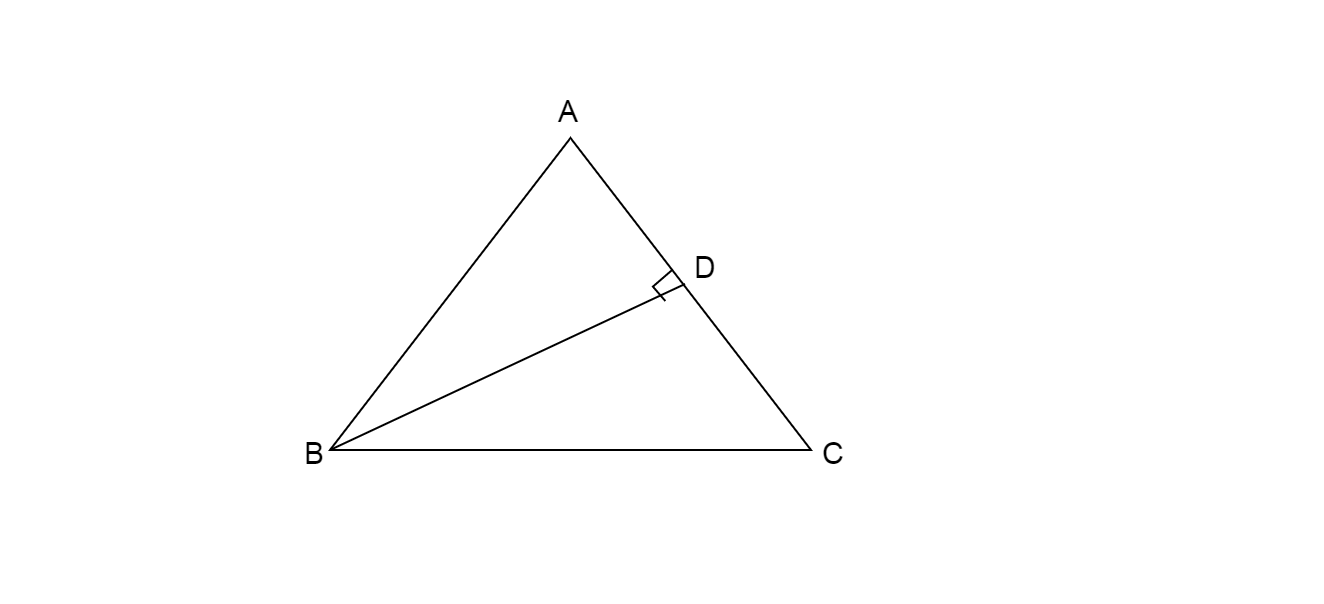
In an isosceles triangle ABC with AB = AC, BD is the perpendicular from B to the side AC, proven that $B{D}^2-C{D}^2=2CD\times AD$.

Answer 1

Hint: The question is related to isosceles triangle. For solving this question, you must know the properties of the isosceles triangle. We know that in the isosceles triangle two of its sides are equal in length.

Complete step by step answer:
Given in the question that perpendicular from B to the side AC is drawn
So, triangle ABD is right angle triangle
According to the right- angle triangle properties we can use Pythagoras theorem
$$\text{Hypotenus}{\text{e}}^2=\text{ Sid}{\text{e}}^2+\text{ Sid}{\text{e}}^2$$
Putting the values
$A{B}^2=B{D}^2+A{D}^2$
As the triangle is isosceles, we know that AB =AC
Replace the AB with AC
$A{C}^2=B{D}^2+A{D}^2$
Here we know that $AC=AD+CD$
$(AD+CD{)}^2=B{D}^2+A{D}^2$
Here applies the formula of $(a+b{)}^2=a^2+b^2+2ab$
$A{D}^2+C{D}^2+2\times AD\times CD=B{D}^2+A{D}^2$
Subtract $A{D}^2$from both the side
$C{D}^2+2\times AD\times CD=B{D}^2$
Now subtract $C{D}^2$from both side
$C{D}^2-C{D}^2+2\times AD\times CD=B{D}^2-C{D}^2$
$\Rightarrow 2\times AD\times CD=B{D}^2-C{D}^2$
Hence,
$\therefore 2AD\times CD=B{D}^2-C{D}^2$

Hence proved.

Note:
Here in type questions students mostly get confused between the side of the triangle. You must know the properties of the particular triangle and when [perpendicular is drawn from any point to line it's always made an angle of ${90}^{\circ }$. For getting the equation mentioned in the question try to simplify your solution. Do not get confused between the naming of the triangle. Here in this question because the perpendicular side AC is divided in two different lengths so we can write AC as the $AC=AD+CD$. Apply the quadrant formula to simplify your equation. Do not get confused between the side and hypotenuse part. Simplify your equation by cancelling and subtracting the same term from the both left hand side and right-hand side.