Question

In an experiment of single slit diffraction pattern, first minimum for red light coincides with first maximum of some other wavelength. If wavelength of red light is $6000{{A}^{o}}$, then wavelength of first maximum will be
\[\begin{align}
  & \text{A}\text{. }3000{{A}^{o}} \\
 & \text{B}\text{. }4000{{A}^{o}} \\
 & \text{C}\text{. 5}000{{A}^{o}} \\
 & \text{D}\text{. 6}000{{A}^{o}} \\
\end{align}\]

Answer 1

Hint: We can observe single slit diffraction when light passes through a single slit of width which is of the order of the wavelength of the incident light. The diffraction pattern is observed at some distance (say$d$) from the slit. We will determine the expression for dark and bright fringes and will calculate the required wavelength of incident light.
Formula used:
Position of dark fringe, $x=n\lambda $
Position of bright fringe, \[x=\left( 2n+1 \right)\dfrac{\lambda }{2}\]

Complete step by step answer:
Diffraction is described as the bending of light around corners such that it spreads out and illuminates areas where it was expected to have a shadow. When the double-slit source in Young’s experiment is replaced by a single narrow slit for observing diffraction pattern, a broad pattern of fringes with a bright region at the centre of the screen is observed. On both sides of the central fringe, there are alternating dark and bright regions. The intensity becomes weaker as we move away from the centre.
Let’s assume the slit width $a\ll D$. Also,$D$ is expressed as the separation between slit and the source.

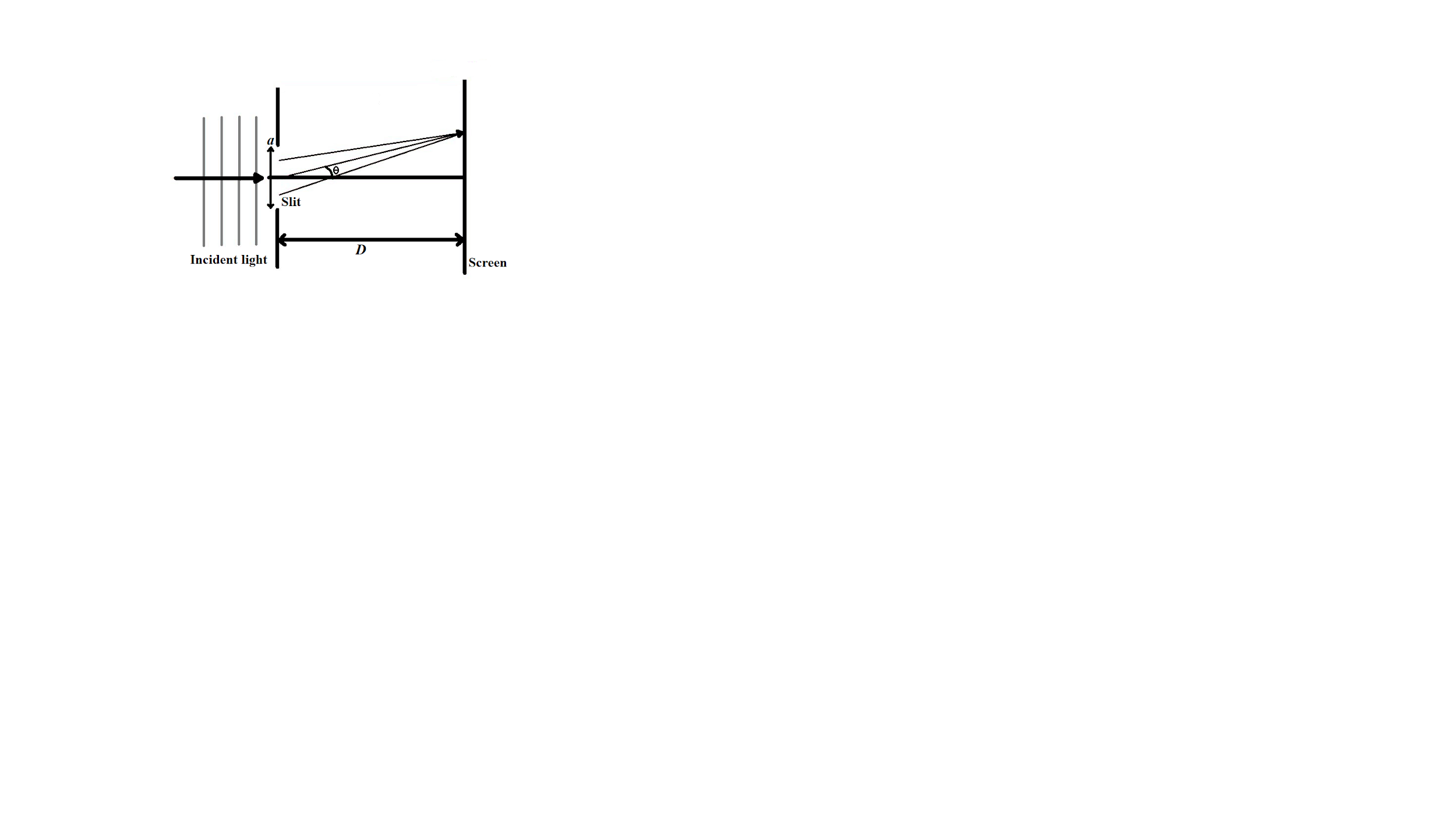
We will find the angular position of any point on the screen by the help of angle$\theta $, measured from the slit centre which divides the slit in $\dfrac{a}{2}$ lengths. To describe the pattern, we will first see the condition for dark fringes observed on the screen. Also, let us divide the split into parts of equal width$\dfrac{a}{2}$. Let us consider a pair of parallel rays that emanate from distances $\dfrac{a}{2}$ from each other as shown in the figure.

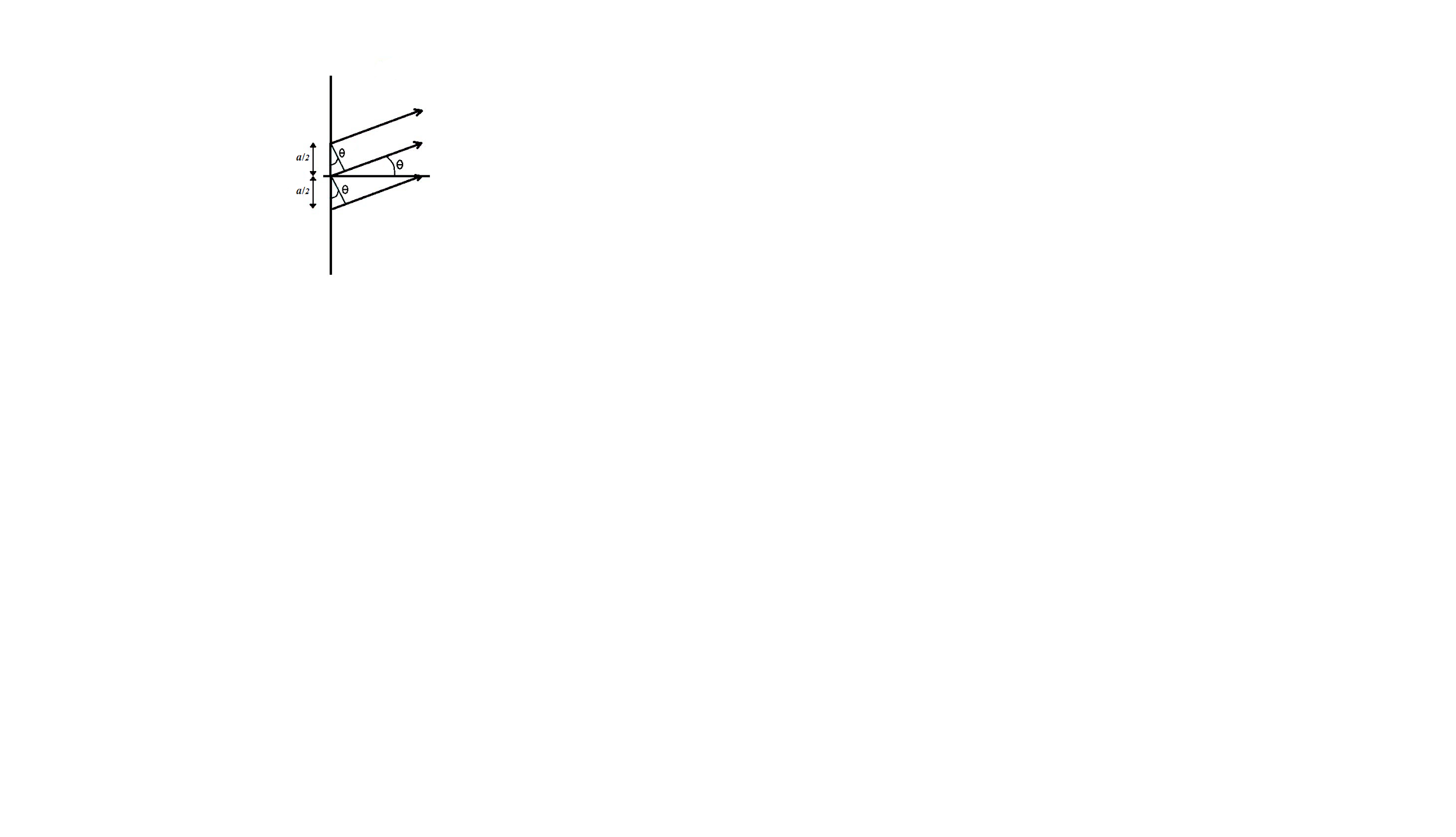
The path difference exhibited by the top two rays shown is:
$\Delta L=\dfrac{a}{2}\sin \theta $
(When, $D$ is very large)
We can consider any number of light ray pairings that start from a distance $\dfrac{a}{2}$ from one another such as the bottom two light rays in the diagram. Any arbitrary pair of rays at a distance $\dfrac{a}{2}$can be considered.
Now,
For a dark fringe, the path difference shall cause destructive interference; the path difference must be out of phase by $\dfrac{\lambda }{2}$($\lambda $ is the wavelength of incident light)
For the first fringe,
$\begin{align}
  & \Delta L=\dfrac{\lambda }{2}=\dfrac{a}{2}\sin \theta \\
 & \lambda =a\sin \theta \\
\end{align}$
For the next fringe, we shall divide the slit into four equal parts of $\dfrac{a}{4}$and apply the same method.
For the bright fringe,
$\lambda =\dfrac{a}{2}\sin \theta $
We can say,
Position of dark fringe is given as,
$x=n\lambda $
Where,
$n=0,1,2....$
$\lambda $is the wavelength of incident light
Position of bright fringe is given as,
\[x=\left( 2n+1 \right)\dfrac{\lambda }{2}\]
Where,
$n=0,1,2....$
$\lambda $is the wavelength of incident light
We are given that the first minimum for red light coincides with first maximum of some other wavelength,
Let the unknown wavelength be $\lambda $
Therefore,
$\left( n+\dfrac{1}{2} \right)\lambda =n{{\lambda }_{red}}$
As given ${{\lambda }_{red}}=6000{{A}^{o}}$
$\begin{align}
  & \lambda =\dfrac{2}{3}\times 6000 \\
 & \lambda =4000{{A}^{o}} \\
\end{align}$
The wavelength of the unknown light is $4000{{A}^{o}}$
Hence, the correct option is B.

Note: Diffraction is evident only when the sources are small enough that are relatively the order of the wavelength of the light. The intensity of different fringes observed on the screen is a function of angle between successive phasors. The position of dark fringes is the even multiple of$\dfrac{\lambda }{2}$, while the position of bright fringes is the odd multiple of$\dfrac{\lambda }{2}$.