Question

In an examination, one hundred candidates took papers in physics and chemistry. Twenty five candidates failed in physics only. Twenty candidates failed in chemistry only. Fifteen candidates failed in both physics and chemistry. A candidate is selected at random. The probability that he failed either in physics or in chemistry but not in both is
$(a).\dfrac{9}{20}$
$(b).\dfrac{3}{5}$
$(c).\dfrac{2}{5}$
$(d).\dfrac{11}{20}$

Answer 1

Hint:
We can make a Venn diagram from the given. Assume $P(A)$ and $P(B)$are the candidates failed in physics and chemistry only. Then $P(A\cap B)$ denotes the candidates failed in both physics and chemistry. From that we can find $P(A\cup B)$ so that is the probability that the randomly selected candidate failed in either in physics or in chemistry but not in both.

Complete step by step solution:
Assume $P(A)$ are the candidates failed in physics.
Candidates failed in physics only is $25$ so we have to find the $P(A)$ value by adding candidate failed in physics only and candidate failed in both physics and chemistry and divide the value by total number of candidates.
 $P(A)=\dfrac{25+15}{100}$
Assume $P(B)$are the candidates failed in chemistry. Candidates failed in chemistry only are $20$.
Same for $P(B)$ we get,
$P(B) =\dfrac{20+15}{100}$

Then $P(A\cap B)$ denotes the candidates failed in both physics and chemistry. Candidates failed in both physics and chemistry are $15$.
Same for $P(A\cap B)$ we get,$P(A\cap B)=\dfrac{15}{100}$

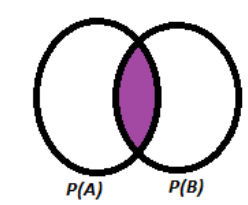
The colored part is the intersection part that is $P(A\cap B)$.
Now we have the formula for union,
 $P(A\cup B)=P(A)+P(B)-P(A\cap B)$
In this formula the intersection will be removed by subtracting so we only get the candidate failed either in physics or chemistry. Apply the value we get,
$\Rightarrow P(A\cup B)=\dfrac{25+15}{100}+\dfrac{20+15}{100}-\dfrac{15}{100}$
Adding the numerator value we get,
$\Rightarrow P(A\cap B)=\dfrac{60}{100}$ dividing the value we get,
$\Rightarrow P(A\cap B)=\dfrac{3}{5}$
The probability that he failed either in physics or in chemistry but not in both is $\dfrac{3}{5}$

Note:
The fact that the two circles do not overlap shows that the two events are mutually exclusive. This means that the probability of A and B happening equals the sum of the probability of A and B.