Question

In an equilateral triangle ABC, the side BC is trisected at D. Prove that \[9A{D^2} = 7A{B^2}\]

Answer 1

Hint: Here we draw a diagram for the situation where we draw a line AD, where D trisects the side BC. We draw an altitude from vertex A to side BC which makes a right angle at the point where it meets the side BC. We find the length of the altitude using Pythagoras theorem in the right triangle formed by the altitude. Assume the length of the side of the equilateral triangle as a variable and write the measures of the trisected part and bisected part of BC. Apply Pythagoras theorem formed by the altitude and the line AD.

Complete step-by-step answer:
We draw an equilateral triangle ABC where all sides are of same length, say ‘a’.
Draw a line AD that trisects the side BC, and draw altitude AE to the side BC making a right angle at point E.

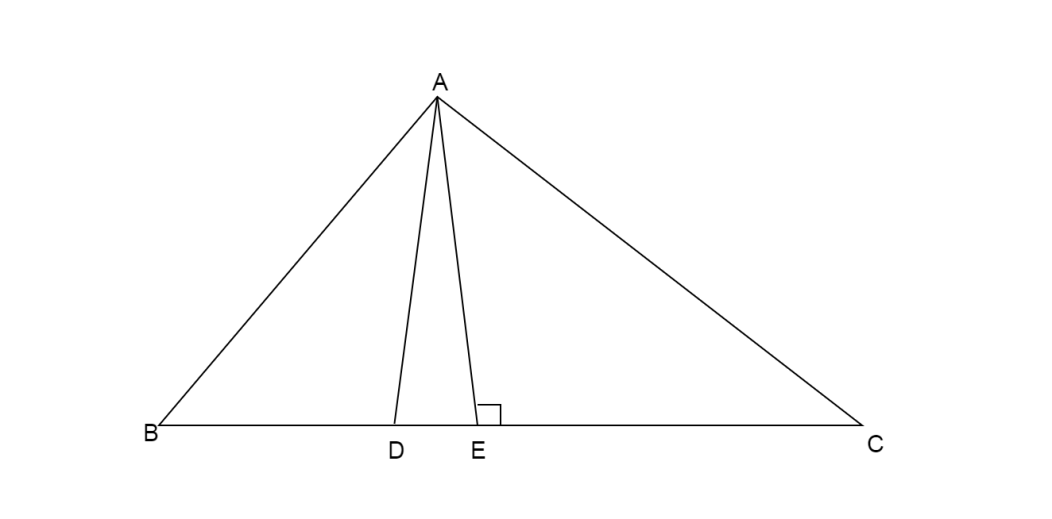
Here \[AB = BC = CA = a\]
AE is the altitude to the side BC, therefore AE bisects BC.
We can write
\[ \Rightarrow BC = BE + EC\]
We know AE bisects BC, then it divides BC into two equal parts. Put \[EC = BE\]
\[ \Rightarrow a = BE + BE\]
\[ \Rightarrow a = 2BE\]
Divide both sides by 2
\[ \Rightarrow BE = \dfrac{a}{2}\] … (1)
Now we know line AD trisects the side BC, then it divided BC into three equal parts.
Then \[BD = \dfrac{{BC}}{3}\]
\[ \Rightarrow BD = \dfrac{a}{3}\] … (2)
Now we know altitude makes right angle at E.
In \[\vartriangle ABE\], apply Pythagoras theorem
\[A{B^2} = B{E^2} + A{E^2}\]
_{Substitute the value of} \[AB = a,BE = \dfrac{a}{2}\]
\[ \Rightarrow {(a)^2} = {(\dfrac{a}{2})^2} + A{E^2}\]
Shift all values with variable a to one side of the equation.
\[ \Rightarrow {a^2} - \dfrac{{{a^2}}}{4} = A{E^2}\]
Take LCM on LHS of the equation
\[ \Rightarrow \dfrac{{4{a^2} - {a^2}}}{4} = A{E^2}\]
\[ \Rightarrow \dfrac{{3{a^2}}}{4} = A{E^2}\]
Take square root on both sides of the equation.
\[ \Rightarrow \sqrt {\dfrac{{3{a^2}}}{4}} = \sqrt {A{E^2}} \]
\[ \Rightarrow \sqrt {\dfrac{{3{a^2}}}{{{2^2}}}} = \sqrt {A{E^2}} \]
Cancel square root with square power on both sides
\[ \Rightarrow \dfrac{{\sqrt 3 a}}{2} = AE\] … (3)
Now we find the length DE by subtracting equation (2) from equation (1).
\[ \Rightarrow BE - BD = DE\]
Substitute the values of \[BE = \dfrac{a}{2},BD = \dfrac{a}{3}\]
\[ \Rightarrow DE = \dfrac{a}{2} - \dfrac{a}{3}\]
Take LCM on RHS
\[ \Rightarrow DE = \dfrac{{3a - 2a}}{6}\]
\[ \Rightarrow DE = \dfrac{a}{6}\]
Since,\[\angle E = {90^ \circ }\]. So, \[\vartriangle AED\]is a right triangle.
We apply Pythagoras theorem in right triangle AED
\[A{D^2} = A{E^2} + D{E^2}\]
Substitute the value of \[\dfrac{{\sqrt 3 a}}{2} = AE\]and \[DE = \dfrac{a}{6}\]
\[ \Rightarrow A{D^2} = {\left( {\dfrac{{\sqrt 3 a}}{2}} \right)^2} + {\left( {\dfrac{a}{6}} \right)^2}\]
\[ \Rightarrow A{D^2} = \dfrac{{3{a^2}}}{4} + \dfrac{{{a^2}}}{{36}}\]
Take LCM on RHs of the equation.
\[ \Rightarrow A{D^2} = \dfrac{{3{a^2} \times 9 + {a^2}}}{{36}}\]
\[ \Rightarrow A{D^2} = \dfrac{{27{a^2} + {a^2}}}{{36}}\]
\[ \Rightarrow A{D^2} = \dfrac{{28{a^2}}}{{36}}\]
Cancel factors from numerator and denominator.
\[ \Rightarrow A{D^2} = \dfrac{{7{a^2}}}{9}\]
Cross multiply the values
\[ \Rightarrow 9A{D^2} = 7{a^2}\]
Put value of \[a = AB\]
\[ \Rightarrow 9A{D^2} = 7A{B^2}\]
Hence proved

Note: * Pythagoras theorem states that in a right angled triangle, the sum of square of base and square of height is equal to square of the hypotenuse.
If we have a right angled triangle, \[\vartriangle ABC\]with right angle, \[\angle B = {90^ \circ }\]

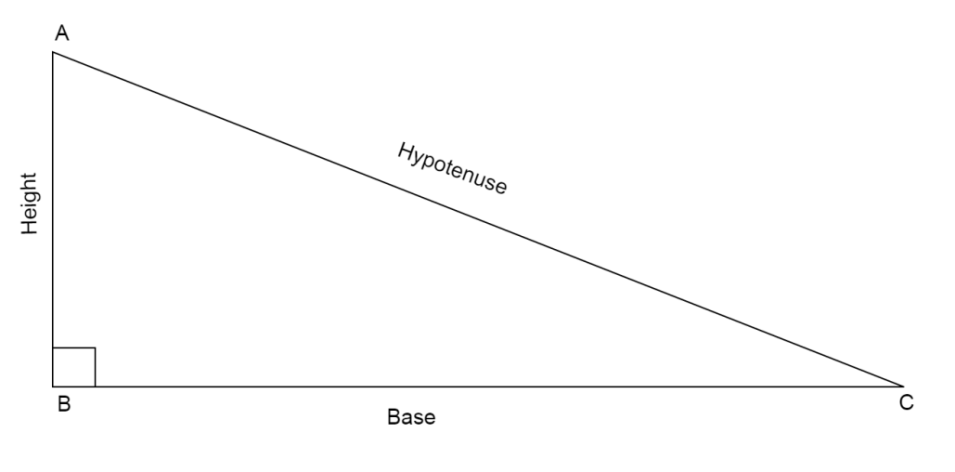
Then using the Pythagoras theorem we can write that \[A{C^2} = A{B^2} + B{C^2}\]