Question

In an equilateral triangle $ABC$, $D$ is a point on side $BC$ such that $4BD=BC$, prove that $16A{{D}^{2}}=13B{{C}^{2}}$.

Answer 1

Hint: First we draw a diagram of equilateral triangle to solve this question. We use the Pythagoras theorem to solve and as we know that the sides of an equilateral triangle are equal in measure, so we find the relation between $AD$ and $BC$.

Complete step by step answer:
We have been given that $ABC$ is an equilateral triangle and $D$ is a point on side $BC$.
We have to prove that $16A{{D}^{2}}=13B{{C}^{2}}$
Let us draw a diagram,

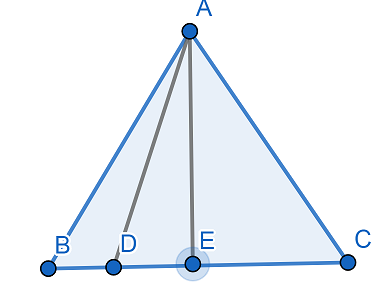
We draw a perpendicular $AE$ to $BC$ i.e. $AE\bot BC$ and $\angle AEC=90{}^\circ ,\angle AEB=90{}^\circ $.
Now, we know that all sides of an equilateral triangle are equal in length so, we have
$AB=BC=AC$
Also, given in the question $4BD=BC$
Or $BD=\dfrac{BC}{4}$
Now, as $\angle AEC=90{}^\circ ,\angle AEB=90{}^\circ $ so, $\Delta AEB$ and $\Delta AED$both are right angled triangle.
Let us first consider $\Delta AEB$, by Pythagoras theorem we can write that,
$A{{B}^{2}}=B{{E}^{2}}+A{{E}^{2}}$
Or we can write $A{{E}^{2}}=A{{B}^{2}}-B{{E}^{2}}............(i)$
Now, let us consider $\Delta AED$, by Pythagoras theorem we can write that
$A{{D}^{2}}=D{{E}^{2}}+A{{E}^{2}}$
Or we can write $A{{E}^{2}}=A{{D}^{2}}-D{{E}^{2}}............(ii)$
When we equate both equation (i) and equation (ii), we get
$A{{B}^{2}}-B{{E}^{2}}=A{{D}^{2}}-D{{E}^{2}}$
\[\Rightarrow A{{B}^{2}}-B{{E}^{2}}+D{{E}^{2}}=A{{D}^{2}}..........(iii)\]
Now, we have
$BE=EC=\dfrac{BC}{2}$ as $AE\bot BC$ and we know that it divides the side $BC$ into two equal parts.
Also, we have $AB=BC=AC$
From, figure we have $DE=BE-BD$ and $BD=\dfrac{BC}{4}$ (given)
Now, substitute all these values in equation (iii), we get
\[\Rightarrow B{{C}^{2}}-{{\left( \dfrac{BC}{2} \right)}^{2}}+{{\left( BE-BD \right)}^{2}}=A{{D}^{2}}\]
\[\begin{align}
  & \Rightarrow B{{C}^{2}}-{{\left( \dfrac{BC}{2} \right)}^{2}}+{{\left( \dfrac{BC}{2}-\dfrac{BC}{4} \right)}^{2}}=A{{D}^{2}} \\
 & \Rightarrow A{{D}^{2}}=B{{C}^{2}}-\dfrac{B{{C}^{2}}}{4}+{{\left( \dfrac{BC}{2} \right)}^{2}}+{{\left( \dfrac{BC}{4} \right)}^{2}}-2\times \dfrac{BC}{2}\times \dfrac{BC}{4} \\
 & \Rightarrow A{{D}^{2}}=B{{C}^{2}}-\dfrac{B{{C}^{2}}}{4}+\dfrac{B{{C}^{2}}}{4}+\dfrac{B{{C}^{2}}}{16}-\dfrac{B{{C}^{2}}}{4} \\
 & \Rightarrow A{{D}^{2}}=\dfrac{16B{{C}^{2}}-4B{{C}^{2}}+4B{{C}^{2}}+B{{C}^{2}}-4B{{C}^{2}}}{16} \\
 & \Rightarrow A{{D}^{2}}=\dfrac{13B{{C}^{2}}}{16} \\
 & \Rightarrow 16A{{D}^{2}}=13B{{C}^{2}} \\
\end{align}\]
Hence proved

Note:
To solve this question we have to substitute all values in terms of $AD$ and $BC$ only. If we substitute other terms, we will not be able to prove the desired relation. The key concept to solve this type of questions is to draw a diagram to understand the problem easily. Students should remember the properties of equilateral triangle to solve this question.