Question

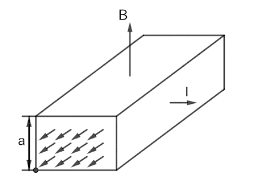
In an electromagnetic pump designed for transferring molten metals a pipe section with metal is located in a uniform magnetic field of induction $ B $ (figure shown above). A current $ I $ is made to flow across this pipe section in the direction perpendicular both to the vector $ \vec{B} $ and to the axis of the pipe. The gauge pressure produced by the pump is $ B=0.10T $ , $ I=100A $ , and $ a=2.0cm $ is $ \dfrac{1}{x}kPa $ . Find $ x $ .

Answer 1

Hint :For the pressure produced by the pump, we can calculate the area from the given dimensions and the force acts on the molten metal because it passes through a uniform magnetic field.

Complete Step By Step Answer:
Let us note down the given data;
Magnitude of the magnetic field $ B=0.10T $
Current flowing through the cross section $ I=100A $
Height of the section $ a=2.0cm $
Length of the block perpendicular to the direction of magnetic field and parallel to the direction of current $ l=? $
Gauge pressure produced by pump $ P=\dfrac{1}{x}kPa $
For an object placed in a uniform magnetic field with its axis making an angle with the magnetic field, if a current is applied across the object in any direction, a force acts on the object which can be expressed as,
 $ \vec{F}=I(\vec{l}\times \vec{B}) $
Here, for the given case, we are concerned with the magnitude of the force only, and the length of the object perpendicular to magnetic field, which is given by,
 $ F=IlB $
For the particular case, this force acting per unit area of the cross section is responsible for the gauge pressure.
The area of the cross section is given as,
 $ A=la $
Now, the gauge pressure is equal to the force acting per unit area, which is mathematically shown as,
 $ P=\dfrac{F}{A} $
Substituting the derived equations,
 $ \therefore P=\dfrac{IlB}{la} $
Canceling the common factor,
 $ \therefore P=\dfrac{IB}{a} $
Substituting the given values,
 $ \therefore P=\dfrac{100A\times 0.10T}{2.0cm} $
Converting the values to SI unit,
 $ \therefore P=\dfrac{100A\times 0.10T}{2.0\times {{10}^{-2}}m} $
Without considering the units,
 $ \therefore P=\dfrac{100\times 0.10}{2.0\times {{10}^{-2}}} $
Writing all the powers together,
 $ \therefore P=\dfrac{1}{2}\times {{10}^{2}}\times {{10}^{-1}}\times {{10}^{2}} $
 $ \therefore P=\dfrac{1}{2}\times {{10}^{3}}Pa $
We know that, $ 1kPa=1000Pa $
  $ \therefore P=\dfrac{1}{2}kPa $
Comparing this value with the given value, we get
 $ x=2 $.

Note :
Here, the force acts on the object due to its orientation. If the object was arranged in such a way, that the length through which the current passes is parallel to the magnetic field, then no force acts on the object.