Question

In an astronomical telescope of normal adjustment a straight black line of length\[L\]is drawn on the inside part of the objective lens. The eyepiece forms a real image of this line. The length of this image is\[l\]. The magnification of the telescope is-
(A). \[\dfrac{L}{l}\]
 (B). \[\dfrac{L}{l}+1\]
(C). \[\dfrac{L}{l}-1\]
 (D). \[\dfrac{L+1}{L-1}\]

Answer 1

Hint: Telescope in normal adjustment means the final image is formed at infinity. The magnification in a telescope is given by the ratio of focal length of objective lens to the focal length of eye-piece. Also for a lens, the magnification is the ratio of image distance to object distance. Here magnification at eye piece is the magnification of the lens.

Formula used:
$M=\dfrac{{{h}_{i}}}{{{h}_{o}}}$
$M=-\dfrac{{{f}_{o}}}{{{f}_{e}}}$
$\dfrac{-{{f}_{e}}}{{{f}_{e}}+u}=\dfrac{{{h}_{i}}}{{{h}_{o}}}$

Complete step by step answer:
A telescope is a device which is used to view far off objects. It is made of a combination of lenses, mirrors or both. In normal adjustment, the final image is formed at infinity.
Magnification is the ratio of image height to object height. It is given by-
$M=\dfrac{{{h}_{i}}}{{{h}_{o}}}$
Here, $M$is the magnification
${{h}_{i}}$is the height of image
${{h}_{o}}$is the height of object

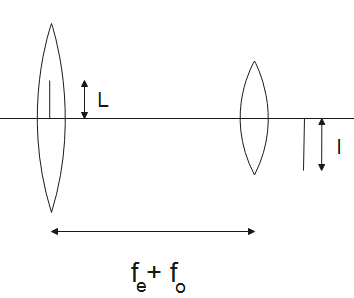
In a telescope, magnification in normal adjustment is-
$M=-\dfrac{{{f}_{o}}}{{{f}_{e}}}$ --- (1)
A telescope contains two lenses, an objective lens and an eye piece. The line of length $L$ is made on the objective lens, its image will be formed by the eye piece. Magnification in eye piece is given by-
$\dfrac{-{{f}_{e}}}{{{f}_{e}}+u}=\dfrac{{{h}_{i}}}{{{h}_{o}}}$ ---- (2)
Here,${{f}_{e}}$is the focal length of the eye-piece
$u$is the distance of the object from the lens.
As we can see from the figure, $u=-({{f}_{e}}+{{f}_{o}})$ . Substituting in eq (2), we get,
$\begin{align}
  & \dfrac{-{{f}_{e}}}{{{f}_{e}}+[-({{f}_{o}}+{{f}_{e}})]}=\dfrac{l}{L} \\
 & \Rightarrow \dfrac{-{{f}_{e}}}{-{{f}_{o}}}=\dfrac{l}{L} \\
\end{align}$
$\begin{align}
  & \Rightarrow \dfrac{{{f}_{e}}}{{{f}_{o}}}=\dfrac{l}{L} \\
 & \therefore \dfrac{{{f}_{o}}}{{{f}_{e}}}=\dfrac{L}{l} \\
\end{align}$
$M=-\dfrac{{{f}_{o}}}{{{f}_{e}}}=-\dfrac{L}{l}$
Therefore, the magnification of the telescope is $\dfrac{L}{l}$ and the negative sign indicates that the image formed is inverted.

So, the correct answer is “Option A”.

Note: In a telescope, the objective lens is much larger than the eye-piece so that it can collect the maximum light to form images of far off objects. First image is made by the objective lens, which acts as an object for the eye-piece. So, the final image is formed by the eye-piece. According to the formula for magnification, \[{{f}_{o}}\] should be greater than \[{{f}_{e}}\] to have better magnification.