Question

In a Young’s double slit experiment, the fringe pattern is observed on a screen placed at a distance \[D\]. The slits are separated by d and are illuminated by light of wavelength \[\lambda \]. The distance from the central point, where the intensity falls to half the maximum is_____________
$\left( {\text{A}} \right){\text{ }}\dfrac{{\lambda {\text{D}}}}{{3{\text{d}}}}$
$\left( {\text{B}} \right){\text{ }}\dfrac{{\lambda {\text{D}}}}{{2{\text{d}}}}$
$\left( {\text{C}} \right){\text{ }}\dfrac{{\lambda {\text{D}}}}{{\text{d}}}$
$\left( {\text{D}} \right){\text{ }}\dfrac{{\lambda {\text{D}}}}{{4{\text{d}}}}$

Answer 1

Hint:
1. YDSE is Young’s Double Slit Experiment. YDSE is performed with a monochromatic light source.
2. Coherent source of light: Two sources of light are said to be a coherent source if the phase difference between them is constant and the same frequency.
3. Monochromatic source of light: The light having the same wavelength is called monochromatic light.
4. Interference of light: When two monochromatic light waves are superimposed on each other, the intensity in the region of superposition gets redistributed, becoming maximum at some points and minimum at others.

Formula used:
${\text{I = }}{{\text{I}}_0}{\text{co}}{{\text{s}}^2}(\dfrac{\theta }{2})$, where \[I = \] Intensity of the light wave, \[{I_0} = \] Intensity of the central fringe,
$\theta = $ Phase difference=$\dfrac{{2\pi }}{\lambda } \times {\text{Path difference}}$, Path difference= $\dfrac{{{\text{dy}}}}{{\text{D}}}$,
Here \[d = \] slits separation, \[y = \] fringe width, \[D = \] screen placed away from the screen.

Complete step by step solution:

     

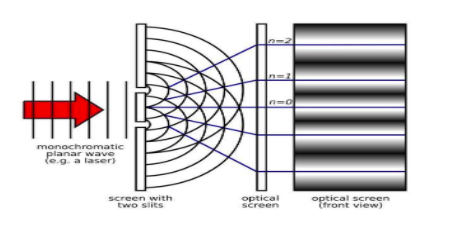
In an interference pattern, the intensities at the points of maxima and minima are directly proportional to the square of the amplitude of the waves. If there is no interference between the light waves from the two sources, then the intensity at every point will be the same and there will be no formation of fringes.
${\text{I = }}{{\text{I}}_0}{\text{co}}{{\text{s}}^2}(\dfrac{\theta }{2})$, it is given that the intensity falls to half the maximum, therefore, we can write that
${\text{I = }}\dfrac{{{{\text{I}}_0}}}{2}$, from this equation, we get the values of \[\theta \], $\theta = \dfrac{\pi }{2}$
Replacing the value of Path difference,
Path difference $ = \dfrac{{\lambda \theta }}{{2\pi }}$$ = \dfrac{\lambda }{{4\pi }}$
Path difference $ = \dfrac{{{\text{dy}}}}{{\text{D}}}$
Equalizing the two equations, we get that, $\dfrac{{{\text{dy}}}}{{\text{D}}}$=$\dfrac{\lambda }{{4\pi }}$
$ \Rightarrow {\text{y = }}\dfrac{{\lambda {\text{D}}}}{{4{\text{d}}}}$

Hence, the correct option is D.

Note:
1. The intensity of light produced by Young’s Double Slit Experiment is calculated as ${\text{I = }}{{\text{I}}_1} + {{\text{I}}_2}{\text{ + 2}}\sqrt {{{\text{I}}_1}{{\text{I}}_2}} {\text{cos}}\theta $
2. Bright fringes or constructive interference are produced when the value of ${\text{cos}}\theta {\text{ = 1}}$, $\theta {\text{ = 0, 2}}\pi, 4\pi, ............$
3. Dark fringes or destructive interference are produced when the value of ${\text{cos}}\theta {\text{ = - 1}}$, $\theta {\text{ = }}\pi {\text{, 3}}\pi {\text{, 5}}\pi, ..............$
4. According to Huygen’s Principle a cylindrical wave front emerges from a point source, in Young’s Double Slit Experiment point source is used so the wave fronts are cylindrical wave fronts.