Question

In a YDSE with identical slits, the intensity of the central bright fringe is \[{I_0}\]. If one of the slits is covered, the intensity at the same point is
A) \[2{I_0}\]
B) \[{I_0}\]
C) \[{I_0}/2\]
D) \[{I_0}/4\]

Answer 1

Hint:To solve this question we need to understand the concept that the intensity of the light is always dependent on the amplitude.

Formula used:
Let the intensity of each slit on the central bright fringe be \[{I_1}\].
Hence, the intensity of the central bright fringe due to the superposition of the light waves coming from two slits,\[{I_0} = {I_1} + {I_1} + 2\sqrt {{I_1}{I_1}} \cos \varphi \]

Complete step by step answer:
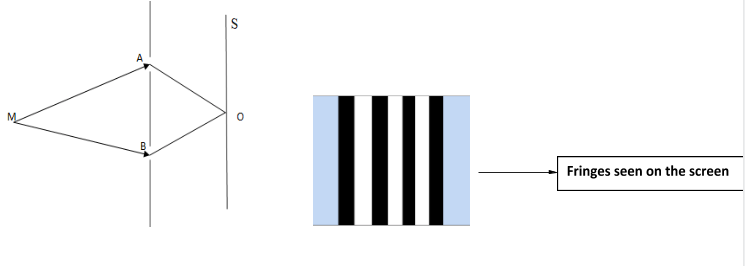
In Young’s double-slit experiment it is shown that light is emitted from a source say M and going through two different points say A and B which are placed at a certain distance from M. A and B act like two secondary sources. If the lab is enough dark then consecutive bright lines and dark lines are seen on the screen S.
The diagram for the above experiment should be,

For two waves of amplitudes \[{a_1}\]and \[{a_2}\] from two coherent sources, the resultant amplitude due to the superposition of the waves, \[A = {a_1} + {a_2} + 2{a_1}{a_2}\cos \varphi \] where, \[\varphi \] is the phase difference.
The intensity of light depends on the amplitude by, \[I \propto {A^2}\].
 Hence if the intensities for the two waves are \[{I_1}\] and \[{I_2}\], then the resultant intensity due to the superposition of the waves, \[I = {I_1} + {I_2} + \sqrt {{I_1}{I_2}} \cos \varphi \].
let the intensity of each slit on the central bright fringe be \[{I_1}\].
Hence, the intensity of the central bright fringe due to the superposition of the light waves coming from two slits,
\[{I_0} = {I_1} + {I_1} + 2\sqrt {{I_1}{I_1}} \cos \varphi \]
The phase difference for the central bright fringe is zero i.e \[\varphi = 0\].
So,
\[{I_0} = {I_1} + {I_1} + 2\sqrt {{I_1}{I_1}} \cos \varphi \]
 \[ \Rightarrow {I_0} = 2{I_1} + 2{I_1}cos0\]
\[ \Rightarrow {I_0} = 2{I_1} + 2{I_1}[\because cos 0 = 1]\]
\[ \Rightarrow {I_0} = 4{I_1}\]
 \[\therefore {I_1} = \dfrac{{{I_0}}}{4}\]
Therefore, the intensity of each slit on the central bright fringe is \[{I_1} = \dfrac{{{I_0}}}{4}\].

Hence option (D) is the correct one.

Notes: In the YDSE if white light is used instead of single coloured light, many colors are shown at the two sides of central white light. Because the lights of different colors and different wavelengths exist in the white light create interference patterns individually. So, the pattern becomes colorful. But for the central position as the colors are incident at the same phase there is shown white bright light.