Question

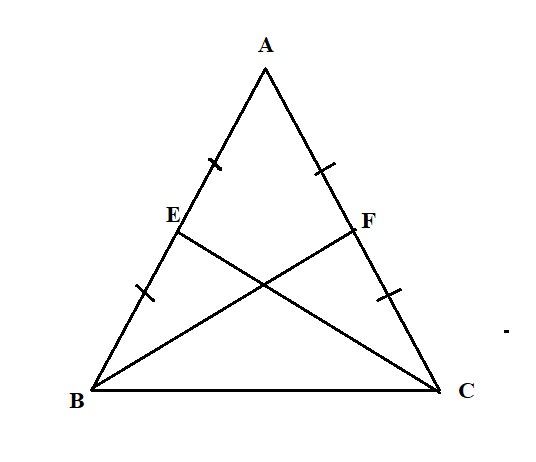
In a triangle $ABC$, if $E$ and $F$ are mid points of the equal sides of $AB$ and $AC$, then show that $BF = CE$

Answer 1

Hint: First use the given condition, $E$ and $F$ are the mid-points of the sides $AB$ and $AC$to get the condition between $AF = AE$. Then, prove triangles $\vartriangle ABF$ and $\vartriangle ACE$ as congruent using side-angle-side criterion. Then, use the CPCT property to get the required result.

Complete step-by-step answer:
We are given that the points $E$ and $F$ are the mid-points of the sides $AB$ and $AC$.
Then, $AE = EB$ and $AF = FC$.
Also, $AB = AC$ as given in the question.
Therefore, $AE = EB = AF = FC$
Next, consider triangles $\vartriangle ABF$ and $\vartriangle ACE$
Here, $AB = AC$, which is a given condition
Also, \[\angle A = \angle A\], which is a common angle in both the triangles.
And $AF = AE$
Thus, triangles are congruent by using side-angle-side criterion
Then, $\vartriangle ABF \cong \vartriangle ACE$
Now, from the corresponding property of congruent triangles, we will have $BF = CE$
Hence, proved.


Note: Congruent triangles have equal sides and equal angles. There are many criteria to prove two triangles equivalent, like SSS( side-side-side), SAS (side-angle-side) , etc. Also, the triangle with two equal sides is an isosceles triangle.