Question

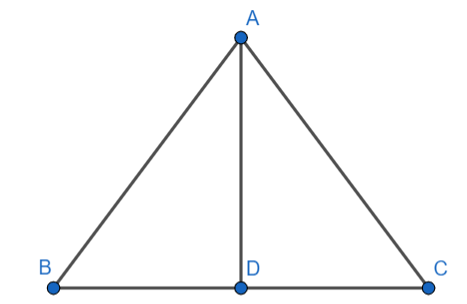
In a triangle ABC, AD is perpendicular to BC. Prove that $A{{B}^{2}}-A{{C}^{2}}=B{{D}^{2}}-C{{D}^{2}}$.

Answer 1

Hint: In a right-angled triangle ABC right-angled at B $A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}$. This is known as Pythagoras theorem. Use Pythagora's theorem in triangles ABD and ACD and equate $A{{D}^{2}}$. Simplify to get the above result.


Complete step by step answer: -
Given: A triangle ABC. $\text{AD}\bot \text{BC}$.
To prove : $A{{B}^{2}}-A{{C}^{2}}=B{{D}^{2}}-C{{D}^{2}}$
Proof:
Using Pythagoras theorem in triangle ABD, we get
$\text{A}{{\text{B}}^{2}}=\text{A}{{\text{D}}^{2}}+\text{B}{{\text{D}}^{2}}$
Subtracting $\text{B}{{\text{D}}^{2}}$ from both sides we get
$\begin{align}
  & \text{A}{{\text{B}}^{2}}-\text{B}{{\text{D}}^{2}}=\text{A}{{\text{D}}^{2}}+\text{B}{{\text{D}}^{2}}-\text{B}{{\text{D}}^{2}} \\
 & \Rightarrow \text{A}{{\text{B}}^{2}}-\text{B}{{\text{D}}^{2}}=\text{A}{{\text{D}}^{2}}\text{ (i)} \\
\end{align}$
Similarly, using Pythagoras theorem in triangle ACD, we get
$\text{A}{{\text{C}}^{2}}=\text{A}{{\text{D}}^{2}}+\text{C}{{\text{D}}^{2}}$
Subtracting $\text{C}{{\text{D}}^{2}}$ from both sides, we get
$\begin{align}
  & \text{A}{{\text{C}}^{2}}-\text{C}{{\text{D}}^{2}}=\text{A}{{\text{D}}^{2}}+\text{C}{{\text{D}}^{2}}-\text{C}{{\text{D}}^{2}} \\
 & \Rightarrow \text{A}{{\text{C}}^{2}}-\text{C}{{\text{D}}^{2}}=\text{A}{{\text{D}}^{2}}\text{ (ii)} \\
\end{align}$
From equation (i) and equation (ii), we get
$\text{A}{{\text{B}}^{2}}-\text{B}{{\text{D}}^{2}}=\text{A}{{\text{C}}^{2}}-\text{C}{{\text{D}}^{2}}$
Adding $\text{B}{{\text{D}}^{2}}-\text{A}{{\text{C}}^{2}}$ on both sides, we get
$\begin{align}
  & \text{A}{{\text{B}}^{2}}-\text{B}{{\text{D}}^{2}}+\text{B}{{\text{D}}^{2}}-\text{A}{{\text{C}}^{2}}=\text{A}{{\text{C}}^{2}}-\text{C}{{\text{D}}^{2}}+\text{B}{{\text{D}}^{2}}-\text{A}{{\text{C}}^{2}} \\
 & \Rightarrow \text{A}{{\text{B}}^{2}}-\text{A}{{\text{C}}^{2}}=\text{B}{{\text{D}}^{2}}-\text{C}{{\text{D}}^{2}} \\
\end{align}$
Hence proved.

Note: Alternatively, we can use trigonometry to prove the above statement
There are six trigonometric ratios defined on an angle of a right-angled triangle, viz sine, cosine,
tangent, cotangent, secant and cosecant.
The sine of an angle is defined as the ratio of the opposite side to the hypotenuse.
The cosine of an angle is defined as the ratio of the adjacent side to the hypotenuse.
The tangent of an angle is defined as the ratio of the opposite side to the adjacent side.
The cotangent of an angle is defined as the ratio of the adjacent side to the opposite side.
The secant of an angle is defined as the ratio of the hypotenuse to the adjacent side.
The cosecant of an angle is defined as the ratio of the hypotenuse to the adjacent side.
If $\text{A}{{\text{B}}^{2}}-\text{A}{{\text{C}}^{2}}=\text{B}{{\text{D}}^{2}}-\text{C}{{\text{D}}^{2}}$ then on dividing both sides by $\text{A}{{\text{D}}^{2}}$ we get
$\dfrac{\text{A}{{\text{B}}^{2}}-\text{A}{{\text{C}}^{2}}}{\text{A}{{\text{D}}^{2}}}=\dfrac{\text{B}{{\text{D}}^{2}}-\text{C}{{\text{D}}^{2}}}{\text{A}{{\text{D}}^{2}}}$
We know that $\dfrac{a-b}{c}=\dfrac{a}{c}-\dfrac{b}{c}$.
Using the above identity, we get
${{\left( \dfrac{\text{AB}}{\text{AD}} \right)}^{2}}-{{\left( \dfrac{\text{AC}}{\text{AD}} \right)}^{2}}={{\left( \dfrac{\text{BD}}{\text{AD}} \right)}^{2}}-{{\left( \dfrac{\text{CD}}{\text{AD}} \right)}^{2}}$
In triangle ABD we have
$\csc \text{B=}\dfrac{\text{AB}}{\text{AD}}$ and $\cot \text{B=}\dfrac{\text{BD}}{\text{AD}}$
In triangle ACD we have
$\csc \text{C=}\dfrac{\text{AC}}{\text{AD}}$ and $\cot \text{C=}\dfrac{\text{CD}}{\text{AD}}$
Substituting these values, we get
${{\csc }^{2}}\text{B-}{{\csc }^{2}}\text{C=}{{\cot }^{2}}\text{B-}{{\cot }^{2}}\text{C}$
Adding ${{\csc }^{2}}\text{C-co}{{\text{t}}^{2}}\text{B}$ on both sides, we get
$\begin{align}
  & {{\csc }^{2}}\text{B-}{{\csc }^{2}}\text{C+}{{\csc }^{2}}\text{C-co}{{\text{t}}^{2}}\text{B=}{{\cot }^{2}}\text{B-}{{\cot }^{2}}\text{C+}{{\csc }^{2}}\text{C-co}{{\text{t}}^{2}}\text{B} \\
 & {{\csc }^{2}}\text{B}-{{\cot }^{2}}\text{B=}{{\csc }^{2}}\text{C-}{{\cot }^{2}}\text{C} \\
\end{align}$
We know that ${{\csc }^{2}}x-{{\cot }^{2}}x=1$
Using we have $1=1$
Which is true.
Hence $\text{A}{{\text{B}}^{2}}-\text{A}{{\text{C}}^{2}}=\text{B}{{\text{D}}^{2}}-\text{C}{{\text{D}}^{2}}$
Hence proved.