Question

In a triangle ABC, ${\text{AB}} = {\text{AC}} = 37$. Let D be a point on BC such that ${\text{BD}} = 7$ ${\text{AD}} = 33$. The length of the CD is.
A) 7
B) 11
C) 40
D) Not determinate

Answer 1

Hint: First construct a perpendicular bisector from the vertex A to the side BC that bisects BC at point M and then use the property of perpendicular bisector and Pythagoras theorem to find the relation in MC and MD, which are applicable in find the required result.

Complete step-by-step answer:
We have given that there is a triangle ABC in which ${\text{AB}} = {\text{AC}} = 37$ and D is a point on BC such that ${\text{BD}} = 7$ and ${\text{AD}} = 33$, and we have to find the length of CD.
First, we will do some construction of perpendicular AM to the base BC which bisect BC in two equal parts.

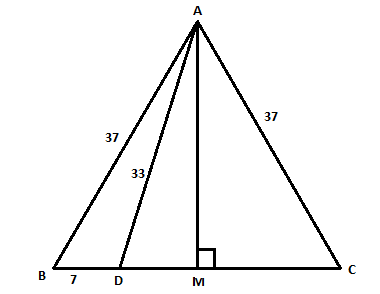
Now, we will take triangle AMC and apply the Pythagoras theorem which gives that: ${\left( {{\text{hypotenuse}}} \right)^2} = {\left( {{\text{base}}} \right)^2} + {\left( {{\text{height}}} \right)^2}$
Now, we will substitute the values of the base, height, and hypotenuse of the triangle AMC.
${\left( {37} \right)^2} = {\left( {{\text{MC}}} \right)^2} + {\left( {{\text{AM}}} \right)^2}$
Which can be written as:
${\left( {{\text{AM}}} \right)^2} = {\left( {37} \right)^2} - {\left( {{\text{MC}}} \right)^2}$ … (1)
Now, we will take the triangle ADM and apply the Pythagoras theorem:
${\left( {{\text{hypotenuse}}} \right)^2} = {\left( {{\text{base}}} \right)^2} + {\left( {{\text{height}}} \right)^2}$
Substitute the values of the base, height, and hypotenuse of the triangle ADM.
${\left( {33} \right)^2} = {\left( {{\text{DM}}} \right)^2} + {\left( {{\text{AM}}} \right)^2}$
Which can be written as:
${\left( {{\text{AM}}} \right)^2} = {\left( {33} \right)^2} - {\left( {{\text{DM}}} \right)^2}$ … (2)
Now, equate both the equation (1) and (2) as both are equal to${\left( {{\text{AM}}} \right)^2}$ :
${\left( {33} \right)^2} - {\left( {{\text{DM}}} \right)^2} = {\left( {37} \right)^2} - {\left( {{\text{MC}}} \right)^2}$
Now, we will take constants on the right-hand side and variables on the left-hand side.
${\left( {{\text{MC}}} \right)^2} - {\left( {{\text{DM}}} \right)^2} = {\left( {37} \right)^2} - {\left( {33} \right)^2}$
Now, we can write this equation in the form of formula${a^2} - {b^2} = \left( {a + b} \right)\left( {a - b} \right)$:
$\left( {{\text{MC + DM}}} \right)\left( {{\text{MC}} - {\text{DM}}} \right) = \left( {37 + 33} \right)\left( {37 - 33} \right)$
$\left( {{\text{MC + DM}}} \right)\left( {{\text{MC}} - {\text{DM}}} \right) = \left( {70} \right)\left( 4 \right)$
We can see from the figure that:
$\left( {{\text{MC + DM}}} \right) = {\text{CD}}$
We can know that \[{\text{MC}} = {\text{BM}}\] because the point M bisects BC into two equal parts.
Now, the equation becomes:
\[\left( {{\text{CD}}} \right)\left( {{\text{BM}} - {\text{DM}}} \right) = \left( {70} \right)\left( 4 \right)\]
Now, we can also see in the figure that\[\left( {{\text{BM}} - {\text{DM}}} \right) = BD\]and the length of $BD$ is given as $7$ unit. So, we obtained:
\[\left( {{\text{CD}}} \right)\left( 7 \right) = \left( {70} \right)\left( 4 \right)\]
\[{\text{CD}} = \dfrac{{70 \times 4}}{7}\]
\[{\text{CD}} = 40\]
Therefore, the length of $CD$ is $40$ unit.

Hence, the option (C) is correct.

Note: We have made a proper construction that is applicable to find the required result. In the given problem, we have constructed a perpendicular bisector from the vertex A to the side BC. After that, we can easily use the property that Perpendicular drawn from the vertex A bisect the side BC in two equal parts.