Question

In a square PQRS, the diagonals bisect at O. Then \[\vartriangle POQ\] is
A. Equilateral
B. Isosceles but not right angled
C. Right angle but not isosceles
D. Isosceles right angled

Answer 1

Hint: Here we draw a square PQRS and use the properties of a square that the diagonals of a square are equal to each other and that diagonals bisect the angles of the square. Using the meaning of an isosceles triangle and right angled triangle we classify which triangle is \[\vartriangle POQ\]
* Square is a 4 sided quadrilateral having all sides equal in length and all four angles as right angles.
* The word bisects means dividing into two equal halves.

Complete step-by-step answer:
We have a square PQRS with sides PQ, QR, RS and SP equal in length and all four angles \[\angle P = \angle Q = \angle R = \angle S = {90^ \circ }\]. The diagonals of square PQRS are PR and QS.

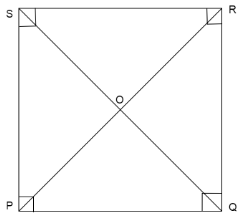
Since, we know that diagonals bisect at point O.
Then we can say the lengths \[OP = OR\] and \[OQ = OS\]
Now since we know that diagonals of a square are equal in lengths
\[ \Rightarrow PR = QS\]
We can write \[PR = OP + OR,QS = OQ + OS\]
\[ \Rightarrow OP + OR = OQ + OS\]
Substituting the value of \[OP = OR\] and \[OQ = OS\]
\[ \Rightarrow OP + OP = OQ + OQ\]
\[ \Rightarrow 2OP = 2OQ\]
Divide both sides of the equation by 2
\[ \Rightarrow \dfrac{{2OP}}{2} = \dfrac{{2OQ}}{2}\]
Cancel the same factors from the numerator and denominator on each side.
\[ \Rightarrow OP = OQ\] … (1)
Therefore, in \[\vartriangle POQ\]we have two sides equal to each other i.e. \[OP = OQ\].
So, \[\vartriangle POQ\] is an isosceles triangle.
Now we know that diagonals of a square bisect the angles of a square.
\[ \Rightarrow \angle OPS = \angle OPQ,\angle OQR = \angle OQP\]
Since we know that all angles of a square are right angles
\[ \Rightarrow \angle P = \angle Q = \angle R = \angle S = {90^ \circ }\]
Now we can write \[\angle P = \angle OPS + \angle OPQ\] … (2)
Substitute \[\angle OPS = \angle OPQ\]and \[\angle P = {90^ \circ }\] in equation (2)
\[ \Rightarrow \angle OPQ + \angle OPQ = {90^ \circ }\]
\[ \Rightarrow 2\angle OPQ = {90^ \circ }\]
Divide both sides of the equation by 2
\[ \Rightarrow \dfrac{{2\angle OPQ}}{2} = \dfrac{{{{90}^ \circ }}}{2}\]
Cancel the same terms from numerator and denominator on both sides of the equation.
\[ \Rightarrow \angle OPQ = {45^ \circ }\]
Also, we can write \[\angle Q = \angle OQR + \angle OQP\] … (3)
Substitute\[\angle OQR = \angle OQP\] and \[\angle Q = {90^ \circ }\] in equation (3)
\[ \Rightarrow \angle OQP + \angle OQP = {90^ \circ }\]
\[ \Rightarrow 2\angle OQP = {90^ \circ }\]
Divide both sides of the equation by 2
\[ \Rightarrow \dfrac{{2\angle OQP}}{2} = \dfrac{{{{90}^ \circ }}}{2}\]
Cancel the same terms from numerator and denominator on both sides of the equation.
\[ \Rightarrow \angle OQP = {45^ \circ }\]
Therefore, in \[\vartriangle POQ\]
\[\angle OPQ = {45^ \circ },\angle OQP = {45^ \circ }\]
Then using the property of sum of all angles of triangle is equal to \[{180^ \circ }\], we can write
\[ \Rightarrow \angle OPQ + \angle OQP + \angle POQ = {180^ \circ }\]
Substituting the values of \[\angle OPQ = {45^ \circ },\angle OQP = {45^ \circ }\]
\[ \Rightarrow {45^ \circ } + {45^ \circ } + \angle POQ = {180^ \circ }\]
Add the terms in LHS
\[ \Rightarrow {90^ \circ } + \angle POQ = {180^ \circ }\]
Shift all the constant terms in degree to RHS of the equation,
\[ \Rightarrow \angle POQ = {180^ \circ } - {90^ \circ }\]
\[ \Rightarrow \angle POQ = {90^ \circ }\]
So, in \[\vartriangle POQ\] one angle is the right angle which makes \[\vartriangle POQ\] as a right angled triangle.
Thus, \[\vartriangle POQ\] is an isosceles right angled triangle.

So, option D is correct.

Note: Students can many times make mistakes while shifting the values from one side of the equation to another side of the equation. Keep in mind that sign changes from positive to negative and vice versa when we shift any value to the opposite side of the equation.