Question

In a right- angled triangle the length of base and perpendicular are 6 cm and 8 cm. What is the length of the hypotenuse?
A) 90 cm
B) 10cm
C) 11cm
D) 12cm

Answer 1

Hint:
In the right angled triangle, the perpendicular and base are given 6 cm and 8 cm respectively. We know that \[\;{\left( {hypotenuse} \right)^2} = {\left( {perpendicular} \right)^2} + {\left( {base} \right)^2}\;\].

Complete step by step solution:

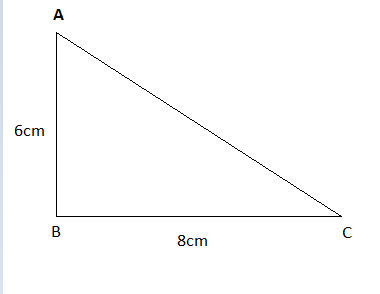
In this given figure AB is perpendicular BC is base and AC is hypotenuse of triangle ABC
We know that, \[\;{\left( {hypotenuse} \right)^2} = {\left( {perpendicular} \right)^2} + {\left( {base} \right)^2}\;\]
\[ \Rightarrow \;{\left( {AC} \right)^2} = {\left( {AB} \right)^2} + {\left( {BC} \right)^2}\;\]
\[ \Rightarrow \;{\left( {AC} \right)^2} = {\left( 6 \right)^2} + {\left( 8 \right)^2}\;\]
\[ \Rightarrow \;{\left( {AC} \right)^2} = 36 + 64 = 100c{m^2}\;\]
Taking root on both side we get
\[ \Rightarrow \;\sqrt {{{\left( {AC} \right)}^2}} = \sqrt {100c{m^2}} \]
$AC = 10cm$

Hence, option (B) is the correct option.

Note:
In triangle ABC there is no any fixed rule for base and perpendicular between two perpendicular lines any of the become base as well as perpendicular. Hypotenuse is the longest side of a right-angled triangle. \[\;{\left( {hypotenuse} \right)^2} = {\left( {perpendicular} \right)^2} + {\left( {base} \right)^2}\;\]