Question

In a regular tetrahedron, the angle between any two faces is
(a) $ {{\sin }^{-1}}\dfrac{1}{3} $
(b) $ {{\cos }^{-1}}\dfrac{1}{3} $
(c) $ {{\tan }^{-1}}\dfrac{1}{\sqrt{3}} $
(d) $ {{\cos }^{-1}}\dfrac{1}{\sqrt{3}} $

Answer 1

Hint: To solve this question, we will first define what a regular tetrahedron is and then to understand better, we will draw a regular tetrahedron of unit size in the 3D space. Using the same tetrahedron in the 3D space, we will find the various points on the figure and try to find the angle between any two faces.

Complete step-by-step answer:
A tetrahedron is a solid figure made of 4 triangles. It is a triangular prism made of 4 triangular faces, 6 straight edges and 4 vertex corners. If all the triangular faces are equilateral triangles, the tetrahedron is known as regular tetrahedron.
Now, we will construct a regular tetrahedron with length of the edge as 1 unit in 3D space.
Suppose one of the vertices is the origin (0, 0, 0). Then A is another edge at A (1, 0, 0). Now, B will be equidistant from A and O and that distance will be 1.
Thus, B lies on the coordinates $ \left( \dfrac{1}{2},\dfrac{\sqrt{3}}{2},0 \right) $ .
C will have a positive value of z – coordinate as it will be the apex. It will also be equidistant from all A, B and O.
Thus, coordinates of C will be $ \left( \dfrac{1}{2},\dfrac{1}{2\sqrt{3}},\sqrt{\dfrac{2}{3}} \right) $
The figure will be as follows:

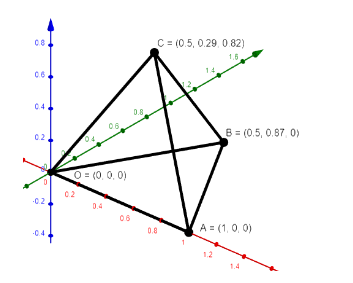
The base of the tetrahedron is OAB and C is the apex of the tetrahedron.
Now, let the midpoint of OA be D. The coordinates of D will be $ \left( \dfrac{1}{2},0,0 \right) $ .
Suppose there is a point E on the place of base OAB and directly under vertex C.
Thus, coordinates of E will be $ \left( \dfrac{1}{2},\dfrac{1}{2\sqrt{3}},0 \right) $ .
The modified figure is as follows:

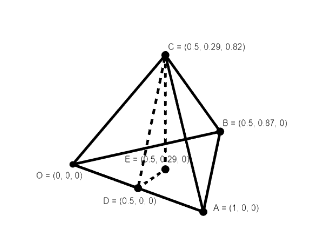
As we can see, $ \angle $ DEC is right angle and triangle DEC is a right angled triangle.
If we find the $ \angle $ CDE, we will find the angle between face OAC and base OAB.
Thus, from triangle DEC, we can say that $ \cos \theta =\dfrac{DE}{CD} $ .
From the distance formula, we can say the that the length of DE is $ \dfrac{1}{2\sqrt{3}} $ and CD is $ \dfrac{\sqrt{3}}{2} $ .
 $ \begin{align}
  & \Rightarrow \cos \theta =\dfrac{\dfrac{1}{2\sqrt{3}}}{\dfrac{\sqrt{3}}{2}} \\
 & \Rightarrow \cos \theta =\dfrac{1}{3} \\
 & \Rightarrow \theta ={{\cos }^{-1}}\dfrac{1}{3} \\
\end{align} $
Therefore, the angle between two faces is $ {{\cos }^{-1}}\dfrac{1}{3} $ .
So, the correct answer is “Option B”.

Note: We can also find the angle by using the vector method. We have to find the vectors of any two sides and then find their normal vectors. After finding the normals, we can use the formula to find the angle between two vectors. But coordinate geometry is much easier for such simple questions, thus we use 3D coordinate geometry.