Question

In a quadrilateral ABCD, if AB is parallel to CD, $\angle D=2\times \angle B$ ; AD = b and CD = a, then the side AB is of length
( a ) $\dfrac{a}{2}+2b$
( a ) $a+2b$
( a ) $2a-b$
( a ) $a+b$

Answer 1

Hint: Basically what we will do here is, we will first value of angle $\angle AMC$ and then using exterior angle sum property we will find the measure of angle $\angle MCB$ in triangle $\vartriangle MCB$. Then using property two angles are equal then sides opposite to equal angles are also equal, we will show that MB = MC and hence solve for the value of AB.

Complete step-by-step solution:

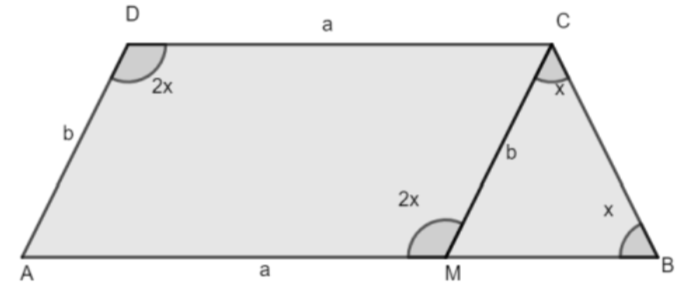
In this question, we have given hint that ABCD is quadrilateral and AB is parallel to CD and angle D is twice of angle B that is $\angle D=2\times \angle B$ and side AD = b and side CD = a, then we have to evaluate the length of side AB.
Now, from figure we can see that AD = b and CM = b and CD = a and AM = a.
As, it is given in the question that, AB is parallel to CD, so we can say that ABCD is a parallelogram.
Also from the figure, we can say that $\angle D=\angle AMC$
Now, let angle B be angle x then as $\angle D=2\times \angle B$ so, angle D will be equals to 2x that is $\angle D=2x$or $\angle AMC=2x$
Now, from the figure in $\vartriangle MCB$,
$\angle AMC=\angle MCB+\angle x$
$2x=\angle MCB+\angle x$ by exterior angle sum property which says that exterior angle equals the sum of the opposite interior angle.
On solving, we get
$\angle MCB=x$
Also, $\angle MCB=\angle B$
So, $\angle MCB=\angle B=x$
In a triangle, if two angles are equal then sides opposite to equal angles are also equal.
So, in $\vartriangle MCB$
$MB = MC$
Now, from figure we can say that
$AB = AM + MB$, and $AM = A$ and $MB = b$, then
Or, $AB = a + b$
Hence, option ( d ) is correct.

Note: It is important that when you solve, proving questions based on a parallelogram, then you must know all the properties of parallelogram and properties of angles. Always make the figure to understand the question visually. The labeling of the diagram should be done properly.