Question

In a quadrilateral ABCD, AO and BO are bisectors of angle A, and angle B respectively. Prove that \[\angle AOB = \dfrac{1}{2}\left\{ {\angle C + \angle D} \right\}\]

Answer 1

Hint: We draw a quadrilateral ABCD with center O. angles A and B are bisected by AO and BO. Apply property of sum of interior angles of quadrilateral to form an equation and property of sum of interior angles of a triangle to form another equation. Equate equations to solve for the required angle.
* Bisector of an angle divides the angle into two equal halves.
* Sum of interior angles of a quadrilateral is \[{360^ \circ }\]
* Sum of interior angles of a triangle is \[{180^ \circ }\]

Complete step by step solution:
We draw a quadrilateral ABCD with center O. OA bisects angle A and OB bisects angle B.

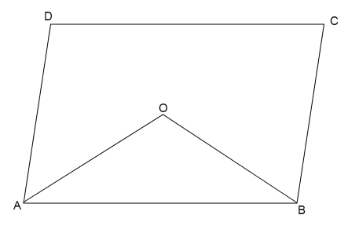
Since OA bisects \[\angle A\]
\[ \Rightarrow \angle OAB = \angle OAD = \dfrac{1}{2}\angle A\]
\[ \Rightarrow 2\angle OAB = \angle A\].........................… (1)
Similarly, OB bisects \[\angle B\]
\[ \Rightarrow \angle OBA = \angle OBC = \dfrac{1}{2}\angle B\]
\[ \Rightarrow 2\angle OBA = \angle B\].......................… (2)
Now we know ABCD is a quadrilateral. Apply property of the sum of interior angles of quadrilateral.
\[ \Rightarrow \angle A + \angle B + \angle C + \angle D = {360^ \circ }\]
Substitute values of angles A and B from equations (1) and (2) in LHS of the equation
\[ \Rightarrow 2\angle OAB + 2\angle OBA + \angle C + \angle D = {360^ \circ }\]
Divide both sides of the equation by 2
\[ \Rightarrow \dfrac{{2\angle OAB + 2\angle OBA + \angle C + \angle D}}{2} = \dfrac{{{{360}^ \circ }}}{2}\]
We can break the terms in LHS as
\[ \Rightarrow \dfrac{{2\angle OAB}}{2} + \dfrac{{2\angle OBA}}{2} + \dfrac{{\angle C + \angle D}}{2} = \dfrac{{{{360}^ \circ }}}{2}\]
Cancel same factors from numerator and denominator
\[ \Rightarrow \angle OAB + \angle OBA + \dfrac{1}{2}\left\{ {\angle C + \angle D} \right\} = {180^ \circ }\].......................… (3)
Now in \[\vartriangle AOB\] apply the property of the sum of interior angles of a triangle.
\[ \Rightarrow \angle OAB + \angle OBA + \angle AOB = {180^ \circ }\]................… (4)
Since RHS of both equations (3) and (4) is equal, we can equate LHS of both the equations.
\[ \Rightarrow \angle OAB + \angle OBA + \dfrac{1}{2}\left\{ {\angle C + \angle D} \right\} = \angle OAB + \angle OBA + \angle AOB\]
Cancel same terms from both sides of the equation
\[ \Rightarrow \dfrac{1}{2}\left\{ {\angle C + \angle D} \right\} = \angle AOB\]
\[\therefore \angle AOB = \dfrac{1}{2}\left\{ {\angle C + \angle D} \right\}\]
Hence Proved

Note: Students might get confused with angle bisectors as they bisect the given angles, they make the mistake of writing the angles formed inside the triangle as equal. Keep in mind we are not given that angle A is equal to angle B, so we cannot say anything about their bisected angles being equal.