Question

In a quadrilateral $ABCD$, $\angle B = {90^ \circ }$, $A{D^2} = A{B^2} + B{C^2} + C{D^2}$, prove that $\angle ACD = {90^ \circ }$.

Answer 1

Hint: In this question we have to prove that in quadrilateral $ABCD$ the angle of $C$ is right angled. That is $\angle ACD = {90^ \circ }$. For that we are going to solve this by using Pythagoras theorem for the triangles in a quadrilateral. And also calculate the angle values by using quadrilaterals, we will get the required result.

Complete step-by-step solution:
Here it is given that the angle of $B$ in quadrilateral is right angled. And $A{D^2} = A{B^2} + B{C^2} + C{D^2}$,
From the given, a quadrilateral $ABCD$

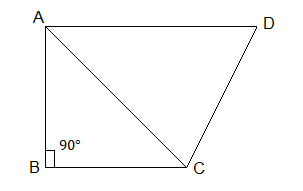
Since, in a given, $\angle ABC = {90^ \circ }$
So, we can apply Pythagoras theorem in $\vartriangle ABC$
By applying we get,
$A{B^2} + B{C^2} = A{C^2} - - - - \left( 1 \right)$
Since, $A{D^2} = A{B^2} + B{C^2} + C{D^2} - - - - \left( 2 \right)$
Substitute the equation (1) into the equation (2), we get,
$ \Rightarrow A{D^2} = A{C^2} + C{D^2} - - - - \left( * \right)$
Let us consider,
Converse of Pythagoras theorem which states that if the square of the length of the longest side of a triangle is equal to the sum of the squares of the other two sides, then the triangle is a right triangle.
If we will apply this in $\vartriangle ACD$, we get,
$ \Rightarrow A{D^2} = A{C^2} + C{D^2}$
Hence, we got the result in equation $\left( * \right)$,
$ \Rightarrow \angle ACD = {90^ \circ }$

$\therefore $ The angle of $C$ is right angled in the given quadrilateral.

Note: In Euclidean plane geometry, a quadrilateral is a polygon with four edges (sides) and four vertices (corners). Quadrilaterals are either simple (not self-intersecting), or complex (self-intersecting, or crossed). Simple quadrilaterals are either convex or concave.
In our problem, the given quadrilateral is the one of the form of right angled trapezium. In Euclidean geometry, a convex quadrilateral with at least one pair of parallel sides is referred to as a trapezium in English outside North America, but as a trapezoid. A right trapezoid (also called right-angled trapezoid) has two adjacent right angles. Right trapezoids are used in the trapezoidal rule for estimating areas under a curve.